



Next: About this document ...
Up: LAPACK95 Users' Guide
Previous: Bibliography
Contents
- absolute error
- Arguments
| Arguments
| Arguments
| Arguments
| Arguments
| Arguments
| Arguments
| Arguments
| Arguments
- accuracy and stability
- Accuracy and Stability
- algorithms
- Bunch-Kaufman
- full storage
- Purpose
| Purpose
| Symmetric Indefinite Linear Systems
- packed storage
- Purpose
| Purpose
| Symmetric Indefinite Linear Systems
- Cholesky decomposition
- Purpose
| Symmetric/Hermitian Positive Definite Linear
- band storage
- Purpose
| Purpose
| Symmetric/Hermitian Positive Definite Linear
- full storage
- Purpose
| Purpose
| Symmetric/Hermitian Positive Definite Linear
- packed storage
- Purpose
| Purpose
| Symmetric/Hermitian Positive Definite Linear
- tridiagonal
- LA_PTSV
| Purpose
- divide and conquer
- Computational Routines for the
- generalized symmetric, band storage
- Purpose
- generalized symmetric, full storage
- Purpose
- generalized symmetric, packed storage
- Purpose
- least squares
- Purpose
- singular value problems
- Purpose
- symmetric tridiagonal
- Purpose
- symmetric, band storage
- Purpose
- symmetric, full storage
- Purpose
- symmetric, packed storage
- Purpose
- Gaussian elimination with row interchanges
- band storage
- Purpose
| Purpose
- dense storage
- Purpose
| Purpose
- tridiagonal
- Purpose
| Purpose
- inverse iteration
- Computational Routines for the
- LDL
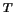 decomposition
decomposition
- full storage
- Purpose
- LDL
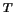 decomposition
decomposition
- full storage
- Purpose
- LDL
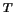 decomposition
decomposition
- packed storage
- Purpose
- LDL
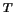 decomposition
decomposition
- packed storage
- Purpose
- Pal-Walker-Kahan
- Computational Routines for the
- QR
- Arguments
| Arguments
- RRR
- Purpose
| Purpose
- Schur decomposition
- see Schur
- UDU
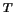 decomposition
decomposition
- full storage
- Purpose
- UDU
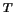 decomposition
decomposition
- full storage
- Purpose
- UDU
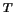 decomposition
decomposition
- packed storage
- Purpose
- UDU
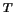 decomposition
decomposition
- packed storage
- Purpose
- ALLOCATABLE attribute
- Design of the LAPACK95
- ALLOCATE statement
- Design of the LAPACK95
- arguments
- assumed-shape arrays
- Array Arguments
- description
- Argument Descriptions
- descriptions
- Argument Descriptions
- illegal value
- Error Handling
- optional
- Design of the LAPACK95
| Optional Arguments
- order of
- Order of Arguments
- rank
- Design of the LAPACK95
- arrays
- allocatable
- Design of the LAPACK95
| Example 1
- assumed-shape
- LAPACK95
| Design of the LAPACK95
| Design of the LAPACK95
| Array Arguments
- empty
- Design of the LAPACK95
- passing subsections
- Design of the LAPACK95
- ATLAS
- LAPACK and the BLAS
| BLAS
| Performance Tables
- automatic allocation
- Design of the LAPACK95
- auxiliary
- enquiry function ILAENV
- Optimal Value of the
- routines
- Levels of Routines
| How to call an
- backward error
- Example (from Program LA_GESVX_EXAMPLE)
| Example (from Program LA_GBSVX_EXAMPLE)
| Example (from Program LA_PPSVX_EXAMPLE)
| Example (from Program LA_PTSVX_EXAMPLE)
| General Linear Systems
| General Linear Systems
| General Linear Systems
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
| Symmetric Indefinite Linear Systems
| Triangular Linear Systems
| Triangular Linear Systems
| Triangular Linear Systems
- bounds
- Linear Equations
- backward transformation
- Computational Routines for the
| Computational Routines for the
- balanced pair of matrices
- Computational Routines for the
- balancing
- Purpose
| Computational Routines for the
- transformation
- Purpose
- band
- form
- see band storage
- storage
- Linear Equations
- scheme
- Example 1
| Example 1
| Example 1
- Basic Linear Algebra Subprograms
- see BLAS
- bidiagonal
- factor
- Computational Routines for the
- form
- Computational Routines for the
- matrices
- Matrix Storage Schemes
| Matrix Storage Schemes
- BLAS
- Preface
| Performance Tables
- library
- BLAS
- model implementation
- BLAS
- optimized
- BLAS
- vendor implementation
- BLAS
- block
- algorithms
- Preface
| Optimal Value of the
- size
- Incorporating Machine Dependencies
| Performance Tables
- bug reports
- Support
- Bunch-Kaufman
- see algorithms
- call LAPACK95 routines
- Example 1
| Example 2
- CD-ROM
- Availability of Software via
- Cholesky
- see algorithms, decomposition and factorization
- column equilibration
- Example (from Program LA_GBSVX_EXAMPLE)
- commercial use
- Commercial Use
- complex
- conjugate pairs
- Nonsymmetric Eigenproblems (NEP)
| Generalized Nonsymmetric Eigenproblems (GNEP)
- Hermitian
- Linear Equations
- Schur factorization
- Nonsymmetric Eigenproblems (NEP)
- symmetric
- Linear Equations
- computation
- failure
- Error Handling
- computational routines
- Problems that LAPACK95 can
| Problems that LAPACK95 can
| Levels of Routines
| Design of Interfaces for
- condition number
- Linear Equations
| Purpose
- eigenvalues
- generalized nonsymmetric
- Purpose
| Purpose
- nonsymmetric
- Arguments
- eigenvectors
- generalized nonsymmetric
- Purpose
| Purpose
- nonsymmetric
- Arguments
- right
- Computational Routines for the
- invariant subspace
- nonsymmetric
- Purpose
- selected eigenvalues
- nonsymmetric
- Purpose
- specified eigenvalues
- Computational Routines for the
- condition number of the system
- complex general
- band
- Purpose
- dense
- Purpose
| General Linear Systems
- triangular band
- Triangular Linear Systems
- triangular matrix
- Triangular Linear Systems
- triangular packed
- Triangular Linear Systems
- tridiagonal
- Purpose
- complex Hermitian
- band storage
- Symmetric/Hermitian Positive Definite Linear
- dense
- Symmetric/Hermitian Positive Definite Linear
- indefinite, full storage
- Purpose
| Symmetric Indefinite Linear Systems
- indefinite, packed storage
- Purpose
| Symmetric Indefinite Linear Systems
- packed storage
- Symmetric/Hermitian Positive Definite Linear
- positive definite, band storage
- Purpose
- positive definite, full storage
- Purpose
- positive definite, packed storage
- Purpose
- positive definite, tridiagonal
- Purpose
- tridiagonal
- Symmetric/Hermitian Positive Definite Linear
- complex symmetric
- indefinite, full storage
- Purpose
| Symmetric Indefinite Linear Systems
- indefinite, packed storage
- Purpose
| Symmetric Indefinite Linear Systems
- general band
- General Linear Systems
- real general
- band
- Purpose
- dense
- Purpose
| General Linear Systems
- triangular band
- Triangular Linear Systems
- triangular matrix
- Triangular Linear Systems
- triangular packed
- Triangular Linear Systems
- tridiagonal
- Purpose
- real symmetric
- dense
- Symmetric/Hermitian Positive Definite Linear
- dense, band storage
- Symmetric/Hermitian Positive Definite Linear
- indefinite, full storage
- Purpose
| Symmetric Indefinite Linear Systems
- indefinite, packed storage
- Purpose
| Symmetric Indefinite Linear Systems
- packed storage
- Symmetric/Hermitian Positive Definite Linear
- positive definite, band storage
- Purpose
- positive definite, full storage
- Purpose
- positive definite, packed storage
- Purpose
- positive definite, tridiagonal
- Purpose
- tridiagonal
- Symmetric/Hermitian Positive Definite Linear
- tridiagonal
- General Linear Systems
- constructing LAPACK routines
- LAPACK and the BLAS
- conventional storage
- Matrix Storage Schemes
- Cosine-Sine decomposition
- Generalized Singular Value Decomposition
- CPU_TIME
- Performance Tables
- CXML
- Performance Tables
- data types
- Data Types and Precision
- debugging
- hints, installation
- Installation Debugging Hints
- release_notes
- Installation Debugging Hints
- decomposition
- Cholesky
- Symmetric/Hermitian Positive Definite Linear
- band storage
- Symmetric/Hermitian Positive Definite Linear
- packed storage
- Symmetric/Hermitian Positive Definite Linear
- tridiagonal
- Symmetric/Hermitian Positive Definite Linear
- singular values
- Purpose
- deflating subspace
- Generalized Nonsymmetric Eigenproblems (GNEP)
| Generalized Nonsymmetric Eigenproblems (GNEP)
| Arguments
| Example (from Program LA_GGESX_EXAMPLE)
- derived types
- Design of the LAPACK95
- diagonal
- block
- Computational Routines for the
| Computational Routines for the
- blocks
- Nonsymmetric Eigenproblems (NEP)
| Generalized Nonsymmetric Eigenproblems (GNEP)
| Computational Routines for the
- elements
- Symmetric Eigenproblems (SEP)
| Argument Descriptions
- entries
- Generalized Singular Value Decomposition
- matrices
- Symmetric Eigenproblems (SEP)
| Singular Value Decomposition (SVD)
| Generalized Symmetric Definite Eigenproblems
| Generalized Singular Value Decomposition
| Generalized Singular Value Decomposition
- divide and conquer
- Generalized Symmetric Definite Eigenproblems
- driver
- Symmetric Eigenproblems (SEP)
- least squares
- Linear Least Squares (LLS)
| Linear Least Squares (LLS)
- method
- Computational Routines for the
- SVD
- Singular Value Decomposition (SVD)
- DLAMCH
- LA_LAMCH Interfaces
- documentation, structure
- Structure of the Documentation
- driver routines
- Problems that LAPACK95 can
| Problems that LAPACK95 can
| Levels of Routines
| Driver Routines
| Performance Tables
- divide and conquer
- Linear Least Squares (LLS)
| Singular Value Decomposition (SVD)
| Generalized Symmetric Definite Eigenproblems
- expert
- Linear Equations
| Generalized Symmetric Definite Eigenproblems
- generalized
- least squares
- Generalized Linear Least Squares
- nonsymmetric eigenvalue problem
- Generalized Nonsymmetric Eigenproblems (GNEP)
| Generalized Nonsymmetric Eigenproblems (GNEP)
- SVD
- Generalized Singular Value Decomposition
- symmetric definite eigenvalue problem
- Generalized Symmetric Definite Eigenproblems
- linear
- equations
- Linear Equations
- least squares
- Linear Least Squares (LLS)
- nonsymmetric eigenvalue problem
- Nonsymmetric Eigenproblems (NEP)
- simple
- Linear Equations
| Generalized Symmetric Definite Eigenproblems
- effective rank of matrix
- Purpose
- eigenvalue problem
- Problems that LAPACK95 can
- ill-conditioned
- Generalized Nonsymmetric Eigenproblems (GNEP)
- regular
- Generalized Nonsymmetric Eigenproblems (GNEP)
- singular
- Generalized Nonsymmetric Eigenproblems (GNEP)
- eigenvalues
- Symmetric Eigenproblems (SEP)
| Symmetric Eigenproblems (SEP)
- all
- generalized nonsymmetric
- Purpose
- generalized symmetric, band storage
- Purpose
- generalized symmetric, full storage
- Purpose
- generalized symmetric, packed storage
- Purpose
- nonsymmetric
- Purpose
| Purpose
- symmetric tridiagonal
- Purpose
- symmetric, band storage
- Purpose
- symmetric, full storage
- Purpose
- symmetric, packed storage
- Purpose
- approximate
- generalized symmetric, band storage
- Arguments
- generalized symmetric, full storage
- Arguments
| Arguments
- symmetric tridiagonal
- Arguments
| Arguments
- symmetric, band storage
- Arguments
- symmetric, full storage
- Arguments
| Arguments
- symmetric, packed storage
- Arguments
- condition number
- nonsymmetric
- Purpose
| Arguments
- divide and conquer method
- Computational Routines for the
- generalized
- Computational Routines for the
- ordering of
- Generalized Nonsymmetric Eigenproblems (GNEP)
- nontrivial
- Generalized Singular Value Decomposition
- ordering of
- Nonsymmetric Eigenproblems (NEP)
- Pal-Walker-Kahan algorithm
- Computational Routines for the
- reciprocal condition numbers
- Computational Routines for the
- selected
- complex Hermitian
- Computational Routines for the
- generalized nonsymmetric
- Purpose
| Purpose
| Purpose
- generalized symmetric, band storage
- Purpose
- generalized symmetric, full storage
- Purpose
- generalized symmetric, packed storage
- Purpose
- nonsymmetric
- Purpose
| Purpose
- real symmetric
- Computational Routines for the
- symmetric tridiagonal
- Purpose
| Purpose
- symmetric, band storage
- Purpose
- symmetric, full storage
- Purpose
| Purpose
- symmetric, packed storage
- Purpose
- selected cluster
- Computational Routines for the
| Computational Routines for the
- symmetric
- positive definite tridiagonal matrix
- Computational Routines for the
- tridiagonal matrix
- Computational Routines for the
- trivial
- Generalized Singular Value Decomposition
- eigenvectors
- Symmetric Eigenproblems (SEP)
- all
- generalized nonsymmetric
- Purpose
- generalized symmetric, band storage
- Purpose
- generalized symmetric, full storage
- Purpose
- generalized symmetric, packed storage
- Purpose
- nonsymmetric
- Purpose
| Purpose
- symmetric tridiagonal
- Purpose
- symmetric, band storage
- Purpose
- symmetric, full storage
- Purpose
- symmetric, packed storage
- Purpose
- complex conjugate pairs
- nonsymmetric
- Arguments
| Arguments
- condition number
- nonsymmetric
- Purpose
| Arguments
- left
- Nonsymmetric Eigenproblems (NEP)
| Generalized Nonsymmetric Eigenproblems (GNEP)
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
- generalized
- Computational Routines for the
- nonsymmetric
- Purpose
| Purpose
- NEP
- Nonsymmetric Eigenproblems (NEP)
- normalized
- nonsymmetric
- Purpose
- orthogonal
- generalized symmetric, band storage
- Arguments
- generalized symmetric, full storage
- Arguments
- generalized symmetric, packed storage
- Arguments
- reciprocal condition numbers
- Computational Routines for the
- right
- Nonsymmetric Eigenproblems (NEP)
| Generalized Nonsymmetric Eigenproblems (GNEP)
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
- generalized
- Computational Routines for the
- nonsymmetric
- Purpose
| Purpose
- scaled
- nonsymmetric
- Purpose
| Arguments
| Purpose
- selected
- complex Hermitian
- Computational Routines for the
- generalized nonsymmetric
- Purpose
| Purpose
| Purpose
- generalized symmetric, band storage
- Purpose
- generalized symmetric, full storage
- Purpose
- generalized symmetric, packed storage
- Purpose
- nonsymmetric
- Purpose
| Purpose
- real symmetric
- Computational Routines for the
- symmetric tridiagonal
- Purpose
| Purpose
- symmetric, band storage
- Purpose
- symmetric, full storage
- Purpose
| Purpose
- symmetric, packed storage
- Purpose
- usually the fastest algorithm
- Purpose
| Purpose
- symmetric
- positive definite tridiagonal matrix
- Computational Routines for the
- tridiagonal matrix
- Computational Routines for the
| Computational Routines for the
- EISPACK
- Preface
- elementary reflectors
- Computational Routines for the
- elimination
- see also factorization or decomposition in algorithms
- equality-constrained least squares
- Generalized Linear Least Squares
- equilibration
- Linear Equations
| General Linear Systems
| General Linear Systems
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
- by column
- Example (from Program LA_GBSVX_EXAMPLE)
- complex general
- band
- Purpose
- dense
- Purpose
- complex Hermitian
- positive definite, band storage
- Purpose
- positive definite, full storage
- Purpose
- positive definite, packed storage
- Purpose
- real general
- band
- Purpose
- dense
- Purpose
- real symmetric
- positive definite, band storage
- Purpose
- positive definite, full storage
- Purpose
- positive definite, packed storage
- Purpose
- ERINFO
- Error Handling
| Error Handling
| Error Handling
| Error Handling
- errata
- see release_notes
- error
- bounds
- General Linear Systems
| General Linear Systems
| General Linear Systems
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
| Symmetric Indefinite Linear Systems
| Triangular Linear Systems
| Triangular Linear Systems
| Triangular Linear Systems
- handling
- Design of the LAPACK95
| Error Handling
- routine
- Error Handling
- error bounds for linear systems
- complex general
- band
- Purpose
- dense
- Purpose
- tridiagonal
- Purpose
- complex Hermitian
- indefinite, full storage
- Purpose
- indefinite, packed storage
- Purpose
- positive definite, band storage
- Purpose
- positive definite, full storage
- Purpose
- positive definite, packed storage
- Purpose
- positive definite, tridiagonal
- Purpose
- complex symmetric
- indefinite, full storage
- Purpose
- indefinite, packed storage
- Purpose
- real general
- band
- Purpose
- dense
- Purpose
- tridiagonal
- Purpose
- real symmetric
- indefinite, full storage
- Purpose
- indefinite, packed storage
- Purpose
- positive definite, band storage
- Purpose
- positive definite, full storage
- Purpose
- positive definite, packed storage
- Purpose
- positive definite, tridiagonal
- Purpose
- ESSL
- Performance Tables
- Euclidean norm
- Arguments
| Purpose
- EXAMPLES1 (directory)
- LAPACK95
- EXAMPLES2 (directory)
- LAPACK95
- expert driver
- Symmetric Eigenproblems (SEP)
- description
- Structure of the Documentation
- f77_lapack.mod
- How to call an
| How to call an
- f95_lapack.mod
- How to call an
| How to call an
- factorization
- see also decomposition or elimination in algorithms
- Cholesky
- Arguments
| Example 2 (from Program
| Arguments
| Example 1 (from Program
| Example 2 (from Program
| Arguments
| Symmetric/Hermitian Positive Definite Linear
- band storage
- Symmetric/Hermitian Positive Definite Linear
- packed storage
- Symmetric/Hermitian Positive Definite Linear
- tridiagonal
- Symmetric/Hermitian Positive Definite Linear
- complex Hermitian
- indefinite matrix
- Symmetric Indefinite Linear Systems
- indefinite matrix, packed storage
- Symmetric Indefinite Linear Systems
- complex symmetric
- indefinite matrix
- Symmetric Indefinite Linear Systems
- indefinite matrix, packed storage
- Symmetric Indefinite Linear Systems
- Gauss
- Purpose
- generalized
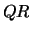
- Purpose
- generalized RQ
- Purpose
- LQ
- Purpose
| Computational Routines for Orthogonal
- LU
- Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| General Linear Systems
| General Linear Systems
| General Linear Systems
- QL
- Computational Routines for Orthogonal
- QR
- Purpose
| Purpose
| Arguments
| Arguments
| Computational Routines for Orthogonal
- with column pivoting
- Computational Routines for Orthogonal
- real symmetric
- indefinite matrix
- Symmetric Indefinite Linear Systems
- indefinite matrix, packed storage
- Symmetric Indefinite Linear Systems
- RQ
- Computational Routines for Orthogonal
- Schur
- Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
- split Cholesky
- Computational Routines for the
- FAQ
- LAPACK95
- Fortran standard
- Preface
- Fortran 77
- Preface
| Performance Issues
| Performance Issues
- Fortran 95
- Preface
| LAPACK95
| Performance Issues
| Performance Issues
- wrappers
- LAPACK95
- forward error
- Example (from Program LA_GESVX_EXAMPLE)
| Example (from Program LA_GBSVX_EXAMPLE)
| Example (from Program LA_PPSVX_EXAMPLE)
| Example (from Program LA_PTSVX_EXAMPLE)
- bounds
- Linear Equations
- Frequently Asked Questions
- see FAQ
- Gauss
- see algorithms and factorization
- Gauss-Markov
- see GLM
- General Gauss-Markov Linear Model Problem
- see GLM
- Generalized
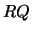 Factorization
Factorization
- see GRQ
- Generalized
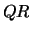 Factorization
Factorization
- see GQR
- generalized eigenproblem
- Computational Routines for the
| Computational Routines for the
- banded, reduction
- Computational Routines for the
- nonsymmetric
- Generalized Nonsymmetric Eigenproblems (GNEP)
- packed form
- Computational Routines for the
- generalized least squares
- Generalized Linear Least Squares
- Generalized Nonsymmetric Eigenvalue Problem
- see GNEP
- generalized Schur
- decomposition
- Generalized Nonsymmetric Eigenproblems (GNEP)
- vectors
- Generalized Nonsymmetric Eigenproblems (GNEP)
- generalized singular value
- Generalized Singular Value Decomposition
| Example 1 (from Program
- Generalized Singular Value Decomposition
- see GSVD
- special cases
- Generalized Singular Value Decomposition
- generalized Sylvester equation
- Computational Routines for the
- Generalized Symmetric Eigenvalue Problem
- see GSEP
- generalized upper Hessenberg form
- Computational Routines for the
- generic
- interface blocks
- F77_LAPACK Generic Interface Blocks
- interfaces
- LAPACK95
| Design of the LAPACK95
- GLM
- Generalized Linear Least Squares
- problem
- Purpose
- GNEP
- Generalized Nonsymmetric Eigenproblems (GNEP)
- GQR
- Generalized Linear Least Squares
| Generalized Linear Least Squares
- GRQ
- Generalized Linear Least Squares
| Generalized Linear Least Squares
- GSEP
- Generalized Symmetric Definite Eigenproblems
- GSVD
- Generalized Singular Value Decomposition
| see Generalized Singular Value Decomposition
| Computational Routines for the
- Hermitian
- Linear Equations
- eigenvalue problem
- Symmetric Eigenproblems (SEP)
- matrices
- Matrix Storage Schemes
- Hessenberg
- upper
- Computational Routines for the
| Computational Routines for the
- generalized form
- Computational Routines for the
- ILAENV
- Optimal Value of the
| Optimal Value of the
| Code for One Version
- illegal argument
- Optional Arguments
- inconsistent shapes
- Error Handling
- indefinite symmetric
- Linear Equations
- Independent Software Vendor
- see ISV
- INFO
- Error Handling
- installation
- Availability and Installation of
- debugging hints
- Installation Debugging Hints
- insufficient memory
- Error Handling
- INTENT attribute
- IN
- Code for One Version
- INOUT
- Code for One Version
- OUT
- Code for One Version
- INTERFACE statement
- LA_SYEV/LA_HEEV
| LA_SYEV/LA_HEEV
| LA_GESV Multiple
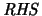 Case
| LA_SYEV/LA_HEEV
| LA_GESV
Case
| LA_SYEV/LA_HEEV
| LA_GESV
- interfaces
- generic
- Design of the LAPACK95
- invalid
- argument
- Error Handling
- shape
- Error Handling
- invariant subspace
- Nonsymmetric Eigenproblems (NEP)
| Generalized Nonsymmetric Eigenproblems (GNEP)
| Purpose
| Purpose
| Computational Routines for the
- inverse of a matrix
- General Linear Systems
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
| Symmetric Indefinite Linear Systems
| Symmetric Indefinite Linear Systems
| Symmetric Indefinite Linear Systems
| Symmetric Indefinite Linear Systems
| Symmetric Indefinite Linear Systems
| Triangular Linear Systems
| Triangular Linear Systems
- ISV
- BLAS
- iterative refinement of the system
- complex general
- band
- Purpose
- dense
- Purpose
- tridiagonal
- Purpose
- complex Hermitian
- indefinite, full storage
- Purpose
- indefinite, packed storage
- Purpose
- positive definite, band storage
- Purpose
- positive definite, full storage
- Purpose
- positive definite, packed storage
- Purpose
- positive definite, tridiagonal
- Purpose
- complex symmetric
- indefinite, full storage
- Purpose
- indefinite, packed storage
- Purpose
- real general
- band
- Purpose
- dense
- Purpose
- tridiagonal
- Purpose
- real symmetric
- indefinite, full storage
- Purpose
- indefinite, packed storage
- Purpose
- positive definite, band storage
- Purpose
- positive definite, full storage
- Purpose
- positive definite, packed storage
- Purpose
- positive definite, tridiagonal
- Purpose
- KIND type parameter
- Data Types and Precision
- la_auxmod.mod
- How to call an
- LA_BDSDC
- Computational Routines for the
- LA_BDSQR
- Computational Routines for the
- LA_GBBRD
- Computational Routines for the
- LA_GBCON
- General Linear Systems
- LA_GBEQU
- General Linear Systems
- LA_GBRFS
- General Linear Systems
- LA_GBSV
- Linear Equations
| LA_GBSV
- LA_GBSVX
- Linear Equations
| LA_GBSVX
- LA_GBTRF
- General Linear Systems
- LA_GBTRS
- General Linear Systems
- LA_GEBAK
- Computational Routines for the
- LA_GEBAL
- Computational Routines for the
- LA_GEBRD
- Computational Routines for the
- LA_GECON
- General Linear Systems
- LA_GEEQU
- General Linear Systems
- LA_GEES
- Nonsymmetric Eigenproblems (NEP)
| Singular Value Decomposition (SVD)
| LA_GEES
- LA_GEESX
- Nonsymmetric Eigenproblems (NEP)
| Singular Value Decomposition (SVD)
| LA_GEESX
- LA_GEEV
- Nonsymmetric Eigenproblems (NEP)
| Singular Value Decomposition (SVD)
| Performance Tables
| Performance Tables
| Performance Tables
| Performance Tables
| LA_GEEV
- LA_GEEVX
- Nonsymmetric Eigenproblems (NEP)
| Singular Value Decomposition (SVD)
| LA_GEEVX
- LA_GEHRD
- Computational Routines for the
- LA_GELQF
- Computational Routines for Orthogonal
- LA_GELS
- Linear Least Squares (LLS)
| Linear Least Squares (LLS)
| LA_GELS
- LA_GELSD
- Linear Least Squares (LLS)
| Linear Least Squares (LLS)
| Linear Least Squares (LLS)
| LA_GELSS / LA_GELSD
- LA_GELSS
- Linear Least Squares (LLS)
| Linear Least Squares (LLS)
| Linear Least Squares (LLS)
| LA_GELSS / LA_GELSD
- LA_GELSY
- Linear Least Squares (LLS)
| Linear Least Squares (LLS)
| Linear Least Squares (LLS)
| LA_GELSY
- LA_GEQLF
- Computational Routines for Orthogonal
- LA_GEQP3
- Computational Routines for Orthogonal
- LA_GEQRF
- Example 2
| Computational Routines for Orthogonal
- LA_GERFS
- General Linear Systems
- LA_GERQF
- Computational Routines for Orthogonal
- LA_GESDD
- Singular Value Decomposition (SVD)
| Singular Value Decomposition (SVD)
| Performance Tables
| Performance Tables
| Performance Tables
| Performance Tables
| LA_GESVD / LA_GESDD
- LA_GESV
- Linear Equations
| Array Arguments
| Example 1
| Performance Tables
| Performance Tables
| Performance Tables
| LA_GESV
- LA_GESVD
- Singular Value Decomposition (SVD)
| Singular Value Decomposition (SVD)
| Performance Tables
| Performance Tables
| Performance Tables
| Performance Tables
| LA_GESVD / LA_GESDD
- LA_GESVX
- Linear Equations
| LA_GESVX
- LA_GETRF
- General Linear Systems
- LA_GETRI
- General Linear Systems
- LA_GETRS
- General Linear Systems
- LA_GGBAK
- Computational Routines for the
- LA_GGBAL
- Computational Routines for the
- LA_GGES
- Generalized Nonsymmetric Eigenproblems (GNEP)
| Generalized Singular Value Decomposition
| LA_GGES
- LA_GGESX
- Generalized Nonsymmetric Eigenproblems (GNEP)
| Generalized Singular Value Decomposition
| LA_GGESX
- LA_GGEV
- Generalized Nonsymmetric Eigenproblems (GNEP)
| Generalized Singular Value Decomposition
| LA_GGEV
- LA_GGEVX
- Generalized Nonsymmetric Eigenproblems (GNEP)
| Generalized Singular Value Decomposition
| LA_GGEVX
- LA_GGGLM
- Generalized Linear Least Squares
| Generalized Linear Least Squares
| LA_GGGLM
- LA_GGHRD
- Computational Routines for the
- LA_GGLSE
- Generalized Linear Least Squares
| LA_GGLSE
- LA_GGSVD
- Generalized Singular Value Decomposition
| Generalized Singular Value Decomposition
| LA_GGSVD
- LA_GGSVP
- Computational Routines for the
- LA_GTCON
- General Linear Systems
- LA_GTRFS
- General Linear Systems
- LA_GTSV
- Linear Equations
| LA_GTSV
- LA_GTSVX
- Linear Equations
| LA_GTSVX
- LA_GTTRF
- General Linear Systems
- LA_GTTRS
- General Linear Systems
- LA_HBEV
- Singular Value Decomposition (SVD)
| LA_SBEV / LA_HBEV /
- LA_HBEVD
- Singular Value Decomposition (SVD)
| LA_SBEV / LA_HBEV /
- LA_HBEVX
- Singular Value Decomposition (SVD)
| LA_SBEVX / LA_HBEVX
- LA_HBGST
- Computational Routines for the
- LA_HBGV
- Generalized Singular Value Decomposition
| LA_SBGV / LA_SBGVD /
- LA_HBGVD
- Generalized Singular Value Decomposition
| LA_SBGV / LA_SBGVD /
- LA_HBGVX
- Generalized Singular Value Decomposition
| LA_SBGVX / LA_HBGVX
- LA_HBTRD
- Computational Routines for the
- LA_HECON
- Symmetric Indefinite Linear Systems
- LA_HEEV
- Singular Value Decomposition (SVD)
| LA_SYEV / LA_HEEV /
- LA_HEEVD
- Singular Value Decomposition (SVD)
| LA_SYEV / LA_HEEV /
- LA_HEEVR
- Singular Value Decomposition (SVD)
| LA_SYEVR / LA_HEEVR
- LA_HEEVX
- Singular Value Decomposition (SVD)
| LA_SYEVX / LA_HEEVX
- LA_HEGST
- Computational Routines for the
- LA_HEGV
- Generalized Singular Value Decomposition
| LA_SYGV /LA_SYGVD / LA_HEGV
- LA_HEGVD
- Generalized Singular Value Decomposition
| LA_SYGV /LA_SYGVD / LA_HEGV
- LA_HEGVX
- Generalized Singular Value Decomposition
| LA_SYGVX / LA_HEGVX
- LA_HERFS
- Symmetric Indefinite Linear Systems
- LA_HESV
- Linear Equations
| LA_SYSV / LA_HESV
- LA_HESVX
- Linear Equations
| LA_SYSVX / LA_HESVX
- LA_HETRD
- Computational Routines for the
- LA_HETRF
- Symmetric Indefinite Linear Systems
- LA_HETRI
- Symmetric Indefinite Linear Systems
- LA_HETRS
- Symmetric Indefinite Linear Systems
- LA_HGEQZ
- Computational Routines for the
- LA_HPCON
- Symmetric Indefinite Linear Systems
- LA_HPEV
- Singular Value Decomposition (SVD)
| LA_SPEV / LA_HPEV /
- LA_HPEVD
- Singular Value Decomposition (SVD)
| LA_SPEV / LA_HPEV /
- LA_HPEVX
- Singular Value Decomposition (SVD)
| LA_SPEVX / LA_HPEVX
- LA_HPGST
- Computational Routines for the
- LA_HPGV
- Generalized Singular Value Decomposition
| LA_SPGV / LA_SPGVD /
- LA_HPGVD
- Generalized Singular Value Decomposition
| LA_SPGV / LA_SPGVD /
- LA_HPGVX
- Generalized Singular Value Decomposition
| LA_SPGVX / LA_HPGVX
- LA_HPRFS
- Symmetric Indefinite Linear Systems
- LA_HPSV
- Linear Equations
| LA_SPSV / LA_HPSV
- LA_HPSVX
- Linear Equations
| LA_SPSVX / LA_HPSVX
- LA_HPTRD
- Computational Routines for the
- LA_HPTRF
- Symmetric Indefinite Linear Systems
- LA_HPTRI
- Symmetric Indefinite Linear Systems
- LA_HPTRS
- Symmetric Indefinite Linear Systems
- LA_HSEIN
- Computational Routines for the
- LA_HSEQR
- Computational Routines for the
- LA_LAMCH
- Machine Dependent Constants (Function
| LA_LAMCH Interfaces
| Arguments
| Arguments
| Arguments
| Arguments
| Arguments
| Arguments
| Arguments
| Arguments
| Arguments
- LA_OPGTR
- Computational Routines for the
- LA_OPMTR
- Computational Routines for the
- LA_ORGBR
- Computational Routines for the
- LA_ORGLQ
- Computational Routines for Orthogonal
- LA_ORGQL
- Computational Routines for Orthogonal
- LA_ORGQR
- Computational Routines for Orthogonal
- LA_ORGRQ
- Computational Routines for Orthogonal
- LA_ORGTR
- Computational Routines for the
- LA_ORMBR
- Computational Routines for the
- LA_ORMHR
- Computational Routines for the
- LA_ORMLQ
- Computational Routines for Orthogonal
- LA_ORMQL
- Computational Routines for Orthogonal
- LA_ORMQR
- Computational Routines for Orthogonal
- LA_ORMRQ
- Computational Routines for Orthogonal
- LA_ORMRZ
- Computational Routines for Orthogonal
- LA_ORMTR
- Computational Routines for the
- LA_PBCON
- Symmetric/Hermitian Positive Definite Linear
- LA_PBEQU
- Symmetric/Hermitian Positive Definite Linear
- LA_PBRFS
- Symmetric/Hermitian Positive Definite Linear
- LA_PBSTF
- Computational Routines for the
- LA_PBSV
- Linear Equations
| LA_PBSV
- LA_PBSVX
- Linear Equations
| LA_PBSVX
- LA_PBTRF
- Symmetric/Hermitian Positive Definite Linear
- LA_PBTRS
- Symmetric/Hermitian Positive Definite Linear
- LA_POCON
- Symmetric/Hermitian Positive Definite Linear
- LA_POEQU
- Symmetric/Hermitian Positive Definite Linear
- LA_PORFS
- Symmetric/Hermitian Positive Definite Linear
- LA_POSV
- Linear Equations
| Optional Arguments
| LA_POSV
- LA_POSVX
- Linear Equations
| LA_POSVX
- LA_POTRF
- Symmetric/Hermitian Positive Definite Linear
- LA_POTRI
- Symmetric/Hermitian Positive Definite Linear
- LA_POTRS
- Symmetric/Hermitian Positive Definite Linear
- LA_PPCON
- Symmetric/Hermitian Positive Definite Linear
- LA_PPEQU
- Symmetric/Hermitian Positive Definite Linear
- LA_PPRFS
- Symmetric/Hermitian Positive Definite Linear
- LA_PPSV
- Linear Equations
| LA_PPSV
- LA_PPSVX
- Linear Equations
| LA_PPSVX
- LA_PPTRF
- Symmetric/Hermitian Positive Definite Linear
- LA_PPTRI
- Symmetric/Hermitian Positive Definite Linear
- LA_PPTRS
- Symmetric/Hermitian Positive Definite Linear
- la_precision.mod
- Data Types and Precision
| How to call an
| How to call an
| How to call an
| Example 1
| Example 2
- LA_PTCON
- Symmetric/Hermitian Positive Definite Linear
- LA_PTEQR
- Computational Routines for the
- LA_PTRFS
- Symmetric/Hermitian Positive Definite Linear
- LA_PTSV
- Linear Equations
| LA_PTSV
- LA_PTSVX
- Linear Equations
| LA_PTSVX
- LA_PTTRF
- Symmetric/Hermitian Positive Definite Linear
- LA_PTTRS
- Symmetric/Hermitian Positive Definite Linear
- LA_SBEV
- Singular Value Decomposition (SVD)
| LA_SBEV / LA_HBEV /
- LA_SBEVD
- Singular Value Decomposition (SVD)
| LA_SBEV / LA_HBEV /
- LA_SBEVX
- Singular Value Decomposition (SVD)
| LA_SBEVX / LA_HBEVX
- LA_SBGST
- Computational Routines for the
- LA_SBGV
- Generalized Singular Value Decomposition
| LA_SBGV / LA_SBGVD /
- LA_SBGVD
- Generalized Singular Value Decomposition
| LA_SBGV / LA_SBGVD /
- LA_SBGVX
- Generalized Singular Value Decomposition
| LA_SBGVX / LA_HBGVX
- LA_SBTRD
- Computational Routines for the
- LA_SPCON
- Symmetric Indefinite Linear Systems
- LA_SPEV
- Singular Value Decomposition (SVD)
| LA_SPEV / LA_HPEV /
- LA_SPEVD
- Singular Value Decomposition (SVD)
| LA_SPEV / LA_HPEV /
- LA_SPEVX
- Singular Value Decomposition (SVD)
| LA_SPEVX / LA_HPEVX
- LA_SPGST
- Computational Routines for the
- LA_SPGV
- Generalized Singular Value Decomposition
| LA_SPGV / LA_SPGVD /
- LA_SPGVD
- Generalized Singular Value Decomposition
| LA_SPGV / LA_SPGVD /
- LA_SPGVX
- Generalized Singular Value Decomposition
| LA_SPGVX / LA_HPGVX
- LA_SPRFS
- Symmetric Indefinite Linear Systems
- LA_SPSV
- Linear Equations
| LA_SPSV / LA_HPSV
- LA_SPSVX
- Linear Equations
| LA_SPSVX / LA_HPSVX
- LA_SPTRD
- Computational Routines for the
- LA_SPTRF
- Symmetric Indefinite Linear Systems
- LA_SPTRI
- Symmetric Indefinite Linear Systems
- LA_SPTRS
- Symmetric Indefinite Linear Systems
- LA_STEBZ
- Computational Routines for the
- LA_STEDC
- Computational Routines for the
- LA_STEGR
- Computational Routines for the
- LA_STEIN
- Computational Routines for the
- LA_STEQR
- Computational Routines for the
- LA_STERF
- Computational Routines for the
- LA_STEV
- Singular Value Decomposition (SVD)
| LA_STEV / LA_STEVD
- LA_STEVD
- Singular Value Decomposition (SVD)
| LA_STEV / LA_STEVD
- LA_STEVR
- Singular Value Decomposition (SVD)
| LA_STEVR
- LA_STEVX
- Singular Value Decomposition (SVD)
| LA_STEVX
- LA_SYCON
- Symmetric Indefinite Linear Systems
- LA_SYEV
- Singular Value Decomposition (SVD)
| Code for One Version
| LA_SYEV / LA_HEEV /
- LA_SYEVD
- Singular Value Decomposition (SVD)
| LA_SYEV / LA_HEEV /
- LA_SYEVR
- Singular Value Decomposition (SVD)
| LA_SYEVR / LA_HEEVR
- LA_SYEVX
- Singular Value Decomposition (SVD)
| LA_SYEVX / LA_HEEVX
- LA_SYGST
- Computational Routines for the
- LA_SYGV
- Generalized Singular Value Decomposition
| LA_SYGV /LA_SYGVD / LA_HEGV
- LA_SYGVD
- Generalized Singular Value Decomposition
| LA_SYGV /LA_SYGVD / LA_HEGV
- LA_SYGVX
- Generalized Singular Value Decomposition
| LA_SYGVX / LA_HEGVX
- LA_SYRFS
- Symmetric Indefinite Linear Systems
- LA_SYSV
- Linear Equations
| LA_SYSV / LA_HESV
- LA_SYSVX
- Linear Equations
| LA_SYSVX / LA_HESVX
- LA_SYTRD
- Computational Routines for the
- LA_SYTRF
- Symmetric Indefinite Linear Systems
- LA_SYTRI
- Symmetric Indefinite Linear Systems
- LA_SYTRS
- Symmetric Indefinite Linear Systems
- LA_TBCON
- Triangular Linear Systems
- LA_TBRFS
- Triangular Linear Systems
- LA_TBTRS
- Triangular Linear Systems
- LA_TGEVC
- Computational Routines for the
- LA_TGEXC
- Computational Routines for the
- LA_TGSEN
- Computational Routines for the
- LA_TGSJA
- Computational Routines for the
- LA_TGSNA
- Computational Routines for the
- LA_TGSYL
- Computational Routines for the
- LA_TPCON
- Triangular Linear Systems
- LA_TPRFS
- Triangular Linear Systems
- LA_TPTRI
- Triangular Linear Systems
- LA_TPTRS
- Triangular Linear Systems
- LA_TRCON
- Triangular Linear Systems
- LA_TREVC
- Computational Routines for the
- LA_TREXC
- Computational Routines for the
- LA_TRRFS
- Triangular Linear Systems
- LA_TRSEN
- Computational Routines for the
- LA_TRSNA
- Computational Routines for the
- LA_TRSYL
- Computational Routines for the
- LA_TRTRI
- Triangular Linear Systems
- LA_TRTRS
- Triangular Linear Systems
- LA_TZRZF
- Computational Routines for Orthogonal
- LA_UNGBR
- Computational Routines for the
- LA_UNGHR
- Computational Routines for the
| Computational Routines for the
- LA_UNGLQ
- Computational Routines for Orthogonal
- LA_UNGQL
- Computational Routines for Orthogonal
- LA_UNGQR
- Computational Routines for Orthogonal
- LA_UNGRQ
- Computational Routines for Orthogonal
- LA_UNGTR
- Computational Routines for the
- LA_UNMBR
- Computational Routines for the
- LA_UNMHR
- Computational Routines for the
- LA_UNMLQ
- Computational Routines for Orthogonal
- LA_UNMQL
- Computational Routines for Orthogonal
- LA_UNMQR
- Computational Routines for Orthogonal
- LA_UNMRQ
- Computational Routines for Orthogonal
- LA_UNMRZ
- Computational Routines for Orthogonal
- LA_UNMTR
- Computational Routines for the
- LA_UPGTR
- Computational Routines for the
- LA_UPMTR
- Computational Routines for the
- LAPACK
- Preface
| Problems that LAPACK95 can
| LAPACK
| Performance Issues
| Performance Tables
- home page
- LAPACK
- Installation Guide
- LAPACK
- library
- LAPACK95
- package
- LAPACK
- test suites
- LAPACK
- Users' Guide
- Symmetric Eigenproblems (SEP)
| Symmetric Eigenproblems (SEP)
| Singular Value Decomposition (SVD)
| Generalized Nonsymmetric Eigenproblems (GNEP)
- LAPACK95
- Preface
| LAPACK95
| Performance Tables
- commercial use of
- Commercial Use
- documentation
- Structure of the Documentation
- driver routines
- Driver Routines
- FAQ
- LAPACK95
- home page
- LAPACK95
- naming
- Design of the LAPACK95
- source code
- LAPACK95
- test suites
- LAPACK95
- leading diagonal blocks
- Computational Routines for the
- least squares solution
- Purpose
| Purpose
| Purpose
| Purpose
- libblas.a
- How to call an
| How to call an
| How to call an
- liblapack.a
- How to call an
| How to call an
| How to call an
| How to call an
- liblapack95.a
- How to call an
| How to call an
| How to call an
- linear equations
- Linear Equations
- linear least squares problem
- Problems that LAPACK95 can
| Linear Least Squares (LLS)
- equality-constrained
- Purpose
- generalized
- Generalized Linear Least Squares
- equality-constrained (LSE)
- Generalized Linear Least Squares
- regression model (GLM)
- Generalized Linear Least Squares
- weighted
- Generalized Linear Least Squares
- LINPACK
- Preface
- LLS (Linear Least Squares)
- Linear Least Squares (LLS)
| Linear Least Squares (LLS)
- LOGICAL FUNCTION SELECT
- Example 2 (from Program
- lower bidiagonal
- form
- Computational Routines for the
- matrix
- Computational Routines for the
- LQ factorization
- Computational Routines for Orthogonal
- LSE
- Generalized Linear Least Squares
| Generalized Linear Least Squares
- problem
- Purpose
- LU factorization
- Levels of Routines
| General Linear Systems
| General Linear Systems
| General Linear Systems
- machine
- constants returned by LA_LAMCH
- Machine Dependent Constants (Function
- dependencies (ILAENV)
- Incorporating Machine Dependencies
- make.inc
- LAPACK95
- matrices
- balancing
- Computational Routines for the
- bidiagonal
- lower
- Computational Routines for the
- upper
- Computational Routines for the
- complex
- unitary
- Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
- complex general
- band
- Purpose
| Purpose
- dense
- Purpose
| Purpose
- tridiagonal
- Purpose
| Purpose
- complex Hermitian
- Computational Routines for the
- band storage
- Computational Routines for the
- block diagonal
 and
and 
- Purpose
- block diagonal
 and
and 
- Purpose
- block diagonal
 and
and 
- Purpose
- block diagonal
 and
and 
- Purpose
- indefinite
- Symmetric Indefinite Linear Systems
- indefinite, full storage
- Purpose
| Purpose
- indefinite, packed storage
- Purpose
| Purpose
| Symmetric Indefinite Linear Systems
- inverse
- Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
- inverse, packed storage
- Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
- packed storage
- Computational Routines for the
- positive definite
- Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
| Computational Routines for the
- positive definite, band storage
- Purpose
| Purpose
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Computational Routines for the
| Computational Routines for the
- positive definite, full storage
- Purpose
| Purpose
- positive definite, packed storage
- Purpose
| Purpose
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
| Computational Routines for the
- positive definite, tridiagonal
- LA_PTSV
| Purpose
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
- complex symmetric
- block diagonal
 and
and 
- Purpose
- block diagonal
 and
and 
- Purpose
- block diagonal
 and
and 
- Purpose
- block diagonal
 and
and 
- Purpose
- indefinite
- Symmetric Indefinite Linear Systems
| Symmetric Indefinite Linear Systems
- indefinite, full storage
- Purpose
| Purpose
- indefinite, packed storage
- Purpose
| Purpose
| Symmetric Indefinite Linear Systems
| Symmetric Indefinite Linear Systems
- inverse
- Symmetric Indefinite Linear Systems
- inverse, packed storage
- Symmetric Indefinite Linear Systems
- effective rank
- Purpose
- full rank
- Purpose
- general
- inverse
- General Linear Systems
- orthogonal
- Computational Routines for Orthogonal
| Computational Routines for Orthogonal
| Computational Routines for Orthogonal
| Computational Routines for Orthogonal
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
- packed storage
- Computational Routines for the
- product
- Computational Routines for Orthogonal
- pencil
- Generalized Nonsymmetric Eigenproblems (GNEP)
- permutation
- Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
- quasi-triangular
- upper
- Computational Routines for the
| Computational Routines for the
- rank deficient
- Purpose
- real general
- band
- Purpose
| Purpose
- dense
- Purpose
| Purpose
- tridiagonal
- Purpose
| Purpose
- real orthogonal
- Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
- real symmetric
- Computational Routines for the
- band storage
- Computational Routines for the
- block diagonal
 and
and 
- Purpose
- block diagonal
 and
and 
- Purpose
- block diagonal
 and
and 
- Purpose
- block diagonal
 and
and 
- Purpose
- indefinite
- Symmetric Indefinite Linear Systems
| Symmetric Indefinite Linear Systems
- indefinite, full storage
- Purpose
| Purpose
- indefinite, packed storage
- Purpose
| Purpose
| Symmetric Indefinite Linear Systems
| Symmetric Indefinite Linear Systems
- inverse
- Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
- inverse, packed storage
- Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
- packed storage
- Computational Routines for the
- positive definite
- Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Computational Routines for the
- positive definite, band storage
- Purpose
| Purpose
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Computational Routines for the
| Computational Routines for the
- positive definite, full storage
- Purpose
| Purpose
- positive definite, packed storage
- Purpose
| Purpose
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Computational Routines for the
- positive definite, tridiagonal
- LA_PTSV
| Purpose
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
| Symmetric/Hermitian Positive Definite Linear
- singular value problems
- complex unitary
- Purpose
- real orthogonal
- Purpose
- Sylvester equation
- Computational Routines for the
- transformation
- generalized singular value
- Purpose
- trapezoidal
- Computational Routines for the
- triangular
- inverse
- Triangular Linear Systems
- packed, inverse
- Triangular Linear Systems
- upper
- Computational Routines for the
- unit lower triangular(L)
- Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| LA_PTSV
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
- unitary
- Computational Routines for Orthogonal
| Computational Routines for Orthogonal
| Computational Routines for Orthogonal
| Computational Routines for Orthogonal
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
- packed storage
- Computational Routines for the
- product
- Computational Routines for Orthogonal
- upper
- Hessenberg
- Computational Routines for the
| Computational Routines for the
- trapezoidal
- Computational Routines for Orthogonal
- triangular (U)
- Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| LA_PTSV
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
- matrix pairs
- eigenvalues
- generalized nonsymmetric
- Purpose
| Purpose
- singular value
- generalized
- Purpose
- megaflops
- Performance Tables
- memory allocation
- Error Handling
- minimum norm
- least squares solution
- Linear Least Squares (LLS)
| Purpose
| Purpose
| Purpose
- solution
- Linear Least Squares (LLS)
| Example 2 (from Program
- mirror repositories of netlib
- Mirror Repositories of netlib
- MODULE
- F77_LAPACK
- How to call an
| How to call an
- F95_LAPACK
- How to call an
| How to call an
- LA_AUXMOD
- How to call an
- LA_PRECISION
- Data Types and Precision
| How to call an
| How to call an
- MODULE statement
- Data Types and Precision
- naming scheme
- Naming Scheme
- computational routine
- Naming Scheme
- driver routine
- Naming Scheme
- LAPACK95
- Design of the LAPACK95
- near-singularity
- Linear Equations
- NEP
- Nonsymmetric Eigenproblems (NEP)
- netlib
- LAPACK95
- mirror repositories
- Mirror Repositories of netlib
- non-negative diagonal elements
- Computational Routines for the
| Computational Routines for the
- nonsymmetric eigenproblem
- generalized
- Generalized Nonsymmetric Eigenproblems (GNEP)
- Nonsymmetric Eigenvalue Problem
- see NEP
- ONLY option
- Code for One Version
- operation counts for LAPACK
- Performance Tables
| Performance Tables
- optimal block size
- Performance Tables
- optional arguments
- LAPACK95
- OPTIONAL attribute
- Design of the LAPACK95
| Code for One Version
- orthogonal
- matrix
- Symmetric Eigenproblems (SEP)
- orthonormal
- basis
- Nonsymmetric Eigenproblems (NEP)
| Purpose
| Purpose
| Computational Routines for the
- columns
- Computational Routines for Orthogonal
| Computational Routines for Orthogonal
- rows
- Computational Routines for Orthogonal
| Computational Routines for Orthogonal
- overdetermined system
- Linear Least Squares (LLS)
| Linear Least Squares (LLS)
- packed
- form
- see packed storage
- storage
- Linear Equations
| Matrix Storage Schemes
- scheme
- Example 1
- partial pivoting
- with row interchanges
- General Linear Systems
| General Linear Systems
| General Linear Systems
- pencil
- see matrices
- performance
- Computers for which LAPACK95
| Computers for which LAPACK95
| LAPACK and the BLAS
| Machine Dependent Constants (Function
| BLAS
| BLAS
| Support
| Performance Issues
| Performance Tables
- pivot growth factor
- Linear Equations
| Example (from Program LA_GESVX_EXAMPLE)
- complex general
- band matrix
- Purpose
- dense matrix
- Purpose
- real general
- band matrix
- Purpose
- dense matrix
- Purpose
- poor performance
- Errors and Poor Performance
| Errors and Poor Performance
| Errors and Poor Performance
- positive definite
- Linear Equations
- precision
- Data Types and Precision
- QL factorization
- Computational Routines for Orthogonal
- QR factorization
- Example 2
| Computational Routines for Orthogonal
- generalized (GQR)
- Generalized Linear Least Squares
- with column pivoting
- Computational Routines for Orthogonal
- quasi-triangular matrix
- Computational Routines for the
| Computational Routines for the
- quotient singular value decomposition
- Generalized Singular Value Decomposition
- rank
- deficient of matrix
- Purpose
- of argument
- Design of the LAPACK95
- README
- LAPACK95
- reciprocal
- condition number
- Example (from Program LA_GESVX_EXAMPLE)
| Example (from Program LA_PPSVX_EXAMPLE)
| Example (from Program LA_PTSVX_EXAMPLE)
| Example (from Program LA_GGESX_EXAMPLE)
| Example (from Program LA_GGEVX_EXAMPLE)
- condition numbers
- Arguments
- pivot growth factor
- Example (from Program LA_GESVX_EXAMPLE)
- reduction
- to bidiagonal form
- Computational Routines for the
- to tridiagonal form
- Example 1 (from Program
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
- reflectors
- see elementary reflectors
- regression, generalized linear
- Generalized Linear Least Squares
- Relatively Robust Representation
- see RRR
- release_notes
- LAPACK
- reliability
- see test suites
- residual sum-of-squares
- Example (from Program LA_GGLSE_EXAMPLE)
- right
- eigenvectors
- Nonsymmetric Eigenproblems (NEP)
- singular vectors
- Example 2 (from Program
- row
- index
- Computational Routines for the
- interchanges
- Example 1
- partial pivoting
- General Linear Systems
| General Linear Systems
| General Linear Systems
- RQ factorization
- Computational Routines for Orthogonal
- generalized (GRQ)
- Generalized Linear Least Squares
- RRR
- driver
- Symmetric Eigenproblems (SEP)
- scaling
- Purpose
- Schur
- complex form
- Purpose
| Purpose
- decomposition
- see factorization
| see factorization
- factorization
- Nonsymmetric Eigenproblems (NEP)
| Nonsymmetric Eigenproblems (NEP)
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Purpose
| Computational Routines for the
| Computational Routines for the
- complex
- Nonsymmetric Eigenproblems (NEP)
- generalized
- Generalized Nonsymmetric Eigenproblems (GNEP)
| Computational Routines for the
| Computational Routines for the
- form
- Computational Routines for the
- generalized
- complex form
- Purpose
| Purpose
| Purpose
| Purpose
- left vectors
- Purpose
| Purpose
| Purpose
| Purpose
- real form
- Purpose
| Purpose
| Purpose
| Purpose
- right vectors
- Purpose
| Purpose
| Purpose
| Purpose
- vectors
- Generalized Nonsymmetric Eigenproblems (GNEP)
| Purpose
| Purpose
| Purpose
| Purpose
- real form
- Purpose
| Purpose
- vectors
- Nonsymmetric Eigenproblems (NEP)
| Nonsymmetric Eigenproblems (NEP)
| Purpose
| Example 2 (from Program
| Purpose
| Computational Routines for the
- selected cluster of eigenvalues
- Computational Routines for the
- SEP
- Symmetric Eigenproblems (SEP)
- simple driver
- Naming Scheme
| Symmetric Eigenproblems (SEP)
| Singular Value Decomposition (SVD)
- single
- shift
- Computational Routines for the
- singular
- Generalized Nonsymmetric Eigenproblems (GNEP)
- vectors
- Singular Value Decomposition (SVD)
| Purpose
| Purpose
| Computational Routines for the
- compact form
- Computational Routines for the
- left
- Singular Value Decomposition (SVD)
| Purpose
- right
- Singular Value Decomposition (SVD)
| Purpose
| Purpose
| Example 2 (from Program
- singular value
- Singular Value Decomposition (SVD)
| Purpose
| Purpose
- bidiagonal factor
- Computational Routines for the
- decomposition
- Singular Value Decomposition (SVD)
| Purpose
| Purpose
- generalized
- Generalized Singular Value Decomposition
| Purpose
- greatest
- Arguments
- problems
- Problems that LAPACK95 can
- singular value decomposition
- Linear Least Squares (LLS)
- generalized
- Generalized Singular Value Decomposition
| Generalized Singular Value Decomposition
| Generalized Singular Value Decomposition
- generalized, special cases
- Generalized Singular Value Decomposition
- quotient
- Generalized Singular Value Decomposition
- SLAMCH
- LA_LAMCH Interfaces
- spectral factorization
- Symmetric Eigenproblems (SEP)
- split Cholesky factorization
- Computational Routines for the
- SRC (directory)
- LAPACK95
- stability
- Accuracy and Stability
- standard
- form
- Computational Routines for the
- packed form
- Computational Routines for the
- storage
- scheme
- Matrix Storage Schemes
- band
- Example 1
- packed
- Example 1
- subspaces
- deflating
- Generalized Nonsymmetric Eigenproblems (GNEP)
- invariant
- Generalized Nonsymmetric Eigenproblems (GNEP)
- SUNPERF
- Performance Tables
- support
- Support
| Support
- SVD
- see singular value decomposition
| Computational Routines for the
| Computational Routines for the
- Sylvester
- equation
- Computational Routines for the
- matrix equation
- Computational Routines for the
- symmetric
- Linear Equations
- eigenproblems (SEP)
- Symmetric Eigenproblems (SEP)
- matrices
- Matrix Storage Schemes
- Symmetric Eigenvalue Problem
- see SEP
- system of linear equations
- Problems that LAPACK95 can
- backward error
- General Linear Systems
| General Linear Systems
| General Linear Systems
| Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
- band storage
- Symmetric/Hermitian Positive Definite Linear
- packed storage
- Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
- triangular band
- Triangular Linear Systems
- triangular matrix
- Triangular Linear Systems
- triangular packed
- Triangular Linear Systems
- tridiagonal
- Symmetric/Hermitian Positive Definite Linear
- condition number
- General Linear Systems
- equilibration
- General Linear Systems
| General Linear Systems
| Symmetric/Hermitian Positive Definite Linear
- band storage
- Symmetric/Hermitian Positive Definite Linear
- packed storage
- Symmetric/Hermitian Positive Definite Linear
- error bounds
- General Linear Systems
| General Linear Systems
| General Linear Systems
| Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
- band storage
- Symmetric/Hermitian Positive Definite Linear
- packed storage
- Symmetric/Hermitian Positive Definite Linear
| Symmetric Indefinite Linear Systems
- triangular band
- Triangular Linear Systems
- triangular matrix
- Triangular Linear Systems
- triangular packed
- Triangular Linear Systems
- tridiagonal
- Symmetric/Hermitian Positive Definite Linear
- scaling
- General Linear Systems
| General Linear Systems
| Symmetric/Hermitian Positive Definite Linear
- band storage
- Symmetric/Hermitian Positive Definite Linear
- packed storage
- Symmetric/Hermitian Positive Definite Linear
- solution
- General Linear Systems
| General Linear Systems
| General Linear Systems
| Symmetric/Hermitian Positive Definite Linear
- band storage
- Symmetric/Hermitian Positive Definite Linear
- packed storage
- Symmetric/Hermitian Positive Definite Linear
- symmetric indefinite
- Symmetric Indefinite Linear Systems
- symmetric indefinite, packed storage
- Symmetric Indefinite Linear Systems
- triangular band
- Triangular Linear Systems
- triangular matrix
- Triangular Linear Systems
- triangular packed
- Triangular Linear Systems
- tridiagonal
- Symmetric/Hermitian Positive Definite Linear
- test suites
- LAPACK95
| LAPACK
| Errors and Poor Performance
- TESTING (directory)
- LAPACK95
- TIMING (directory)
- LAPACK95
- transformation
- backward
- Computational Routines for the
| Computational Routines for the
- equivalence
- orthogonal
- Computational Routines for the
| Computational Routines for the
- unitary
- Computational Routines for the
| Computational Routines for the
- orthogonal
- Purpose
| Computational Routines for Orthogonal
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
- similarity
- orthogonal
- Computational Routines for the
- orthogonal, band storage
- Computational Routines for the
- orthogonal, packed storage
- Computational Routines for the
- unitary
- Computational Routines for the
- unitary, band storage
- Computational Routines for the
- unitary, packed storage
- Computational Routines for the
- unitary
- Purpose
| Computational Routines for Orthogonal
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
| Computational Routines for the
- trapezoidal matrices
- Computational Routines for the
- triangular
- factor
- Cholesky
- Example 2 (from Program
| Example 1 (from Program
| Example 2 (from Program
- matrices
- Matrix Storage Schemes
- tridiagonal
- form
- Levels of Routines
- matrices
- Matrix Storage Schemes
- troubleshooting
- Performance and Troubleshooting
- underdetermined system
- Linear Least Squares (LLS)
| Linear Least Squares (LLS)
- unitary
- matrix
- Symmetric Eigenproblems (SEP)
| Example 1 (from Program
- upper
- bidiagonal
- form
- Computational Routines for the
| Computational Routines for the
- matrix
- Computational Routines for the
- Hessenberg matrix
- Computational Routines for the
| Computational Routines for the
- trapezoidal matrix
- Computational Routines for Orthogonal
- triangular
- form
- Computational Routines for Orthogonal
- matrices
- Computational Routines for the
- USE
- F77_LAPACK
- How to call an
| Code for One Version
- F95_LAPACK
- How to call an
- LA_AUXMOD
- How to call an
| Code for One Version
- LA_PRECISION
- How to call an
| Code for One Version
- DP
- Data Types and Precision
- SP
- Data Types and Precision
- USE statement
- Data Types and Precision
| Data Types and Precision
- vendor supplied BLAS
- BLAS
- weighted linear least squares
- Purpose
- working precision (WP)
- Example 2
- zero-sized array
- Design of the LAPACK95
Susan Blackford
2001-08-19
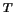 decomposition
decomposition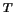 decomposition
decomposition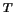 decomposition
decomposition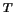 decomposition
decomposition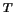 decomposition
decomposition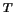 decomposition
decomposition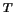 decomposition
decomposition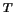 decomposition
decomposition
 and
and 
 and
and 
 and
and 
 and
and 
 and
and 
 and
and 
 and
and 
 and
and 
 and
and 
 and
and 
 and
and 
 and
and 