




Next: Driver Routines for Singular
Up: Generalized Nonsymmetric Eigenvalue Problems
Previous: Arguments
Contents
Index
The results below are computed with
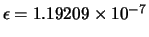 .
.
Arrays A and B on entry:
The call:
CALL LA_GGEVX( A, B, ALPHA, BETA, BALANC='B', LSCALE=LSCALE, &
RSCALE=RSCALE, ABNRM=ABNRM, &
BBNRM=BBNRM, RCONDE=RCONDE, &
RCONDV=RCONDV )
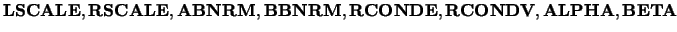 and LAMBDA on exit:
and LAMBDA on exit:
Balancing was not needed.
The 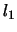 norm of
norm of  is
is
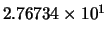 and
the
and
the 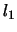 norm of
norm of  is
is
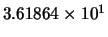 .
.
The reciprocal condition numbers of the eigenvalues are:
The reciprocal condition numbers of the eigenvectors are:





Next: Driver Routines for Singular
Up: Generalized Nonsymmetric Eigenvalue Problems
Previous: Arguments
Contents
Index
Susan Blackford
2001-08-19
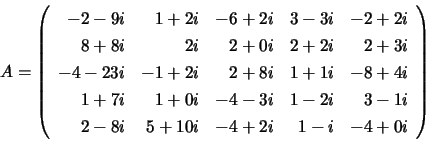
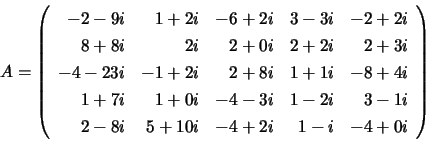
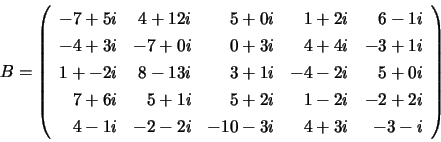


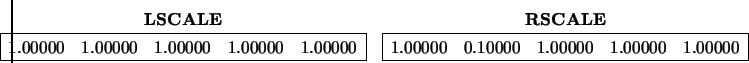
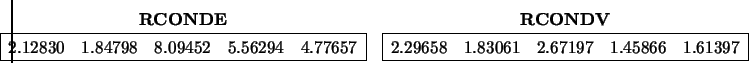


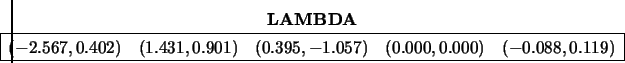
![]() norm of
norm of ![]() is
is
![]() and
the
and
the ![]() norm of
norm of ![]() is
is
![]() .
.