Computational Routines for the Generalized Singular Value Decomposition

LA_GGSVP
Real version.

SUBROUTINE LA_GGSVP( JOBU, JOBV, JOBQ, & 


M, P, N, A, LDA, B, LDB, TOLA, TOLB, K, & 


L, U, LDU, V, LDV, Q, LDQ, IWORK, TAU, & 


WORK, INFO ) 


CHARACTER(LEN=1), INTENT(IN) :: JOBQ, & 


JOBU, JOBV 


INTEGER, INTENT(IN) :: LDA, LDB, LDQ, & 


LDU, LDV, M, N, P 


INTEGER, INTENT(OUT) :: INFO, K, L, & 


IWORK(*) 


REAL(wp), INTENT(IN) :: TOLA, TOLB 


REAL(wp), INTENT(INOUT) :: A(LDA,*), & 


B(LDB,*) 


REAL(wp), INTENT(OUT) :: Q(LDQ,*), TAU(*), & 


U(LDU,*), V(LDV,*), WORK(*) 


where 

wp   ::= KIND(1.0) $\mid$ KIND(1.0D0)

Complex version.

 SUBROUTINE LA_GGSVP( JOBU, JOBV, JOBQ, & 


M, P, N, A, LDA, B, LDB, TOLA, TOLB, K, & 


L, U, LDU, V, LDV, Q, LDQ, IWORK, & 


RWORK, TAU, WORK, INFO ) 


CHARACTER(LEN=1), INTENT(IN) :: JOBQ, & 


JOBU, JOBV 


INTEGER, INTENT(IN) :: LDA, LDB, LDQ, & 


LDU, LDV, M, N, P 


INTEGER, INTENT(OUT) :: INFO, K, L, & 


IWORK(*) 


REAL(wp), INTENT(IN) :: TOLA, TOLB 


REAL(wp), INTENT(IN) :: RWORK(*) 


COMPLEX(wp), INTENT(INOUT) :: A(LDA,*), & 


B(LDB,*) 


COMPLEX(wp), INTENT(OUT) :: Q(LDQ,*), & 


TAU(*), U(LDU,*), V(LDV,*), WORK(*) 


where 

wp   ::= KIND(1.0) $\mid$ KIND(1.0D0)

LA_GGSVP computes orthogonal / unitary matrices 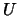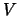$U$, $V$ and $Q$.
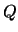References: See  [1] and [9,20].
-----------------------------------

LA_TGSJA
Real and complex versions.

SUBROUTINE LA_TGSJA( JOBU, JOBV, JOBQ, & 


M, P, N, K, L, A, LDA, B, LDB, TOLA, & 


TOLB, ALPHA, BETA, U, LDU, V, LDV, Q, & 


LDQ, WORK, NCYCLE, INFO ) 


CHARACTER(LEN=1), INTENT(IN) :: JOBQ, & 


JOBU, JOBV 


INTEGER, INTENT(IN) :: K, L, LDA, LDB, & 


LDQ, LDU, LDV, M, N, NCYCLE, P 


INTEGER, INTENT(OUT) :: INFO 


REAL(wp), INTENT(IN) :: TOLA, TOLB 


REAL(wp), INTENT(OUT) :: ALPHA(*), & 


BETA(*) 

type(wp), INTENT(INOUT) :: A(LDA,*), & 


B(LDB,*), Q(LDQ,*), U(LDU,*), V(LDV,*) 

type(wp), INTENT(OUT) :: WORK(*) 


where 

type ::= REAL $\mid$ COMPLEX 

wp   ::= KIND(1.0) $\mid$ KIND(1.0D0)

LA_TGSJA computes the generalized singular value decomposition (GSVD) of two real / complex upper triangular (or trapezoidal) matrices $A$ and $B$.
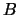References: See  [1] and [9,20].
-----------------------------------