Bibliography

1

E. ANDERSON, Z. BAI, C. BISCHOF, L. S. BLACKFORD, J. DEMMEL, J. DONGARRA, J. DU CROZ, A. GREENBAUM, S. HAMMARLING, A. MCKENNEY, AND D. SORENSEN, LAPACK Users' Guide, Society for Industrial and Applied Mathematics, Philadelphia, PA, third ed., 1999.

2

Z. BAI AND J. W. DEMMEL, Computing the generalized singular value decomposition, SIAM J. Sci. Comp., 14 (1993), pp. 1464-1486.
(Also LAPACK Working Note #46).

3

Z. BAI AND H. ZHA, A new preprocessing algorithm for the computation of the generalized singular value decomposition, SIAM J. Sci. Comp., 14 (1993), pp. 1007-1012.

4

L. S. BLACKFORD AND J. DONGARRA, Installation guide for LAPACK, Computer Science Dept. Technical Report CS-92-151, University of Tennessee, Knoxville, TN, March 1992.
(Also LAPACK Working Note #41).

5

height 2pt depth -1.6pt width 23pt, Quick installation guide for LAPACK on Unix systems, Computer Science Dept. Technical Report CS-94-249, University of Tennessee, Knoxville, TN, September 1994.
(LAPACK Working Note #81).

6

L. S. BLACKFORD, J. DONGARRA, J. DU CROZ, S. HAMMARLING, AND J. WASNIEWSKI, A Fortran 90 Interface for LAPACK, Computer Science Dept. Technical Report CS-96-341, University of Tennessee, Knoxville, TN, 1996.
(Also LAPACK Working Note #117).

7

COMPAQ CORPORATION, Compaq Extended Math Library.
http://www.compaq.com/hpc/software/dxml.html.

8

J. DEMMEL AND W. KAHAN, Computing Small Singular Values of Bidiagonal Matrices with Guaranteed High Relative Accuracy, SIAM J. Sci. Statist. Comput., 11 (1990), pp. 873-912.
Also (LAPACK Working Note # 3: http://www.netlib.org/lapack/lawns/lawn03.ps or http://www.netlib.org/lapack/lawnspdf/lawn03.pdf).

9

J. W. DEMMEL, Applied Numerical Linear Algebra, Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, first ed., 1997.

10

J. W. DEMMEL AND B. KÅGSTR¨OM, Computing stable eigendecompositions of matrix pencils, Lin. Alg. Appl., 88/89 (1987), pp. 139-186.

11

I. DHILLON, A New O(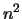$n^2$) Algorithm for the Symmetric Tridiagonal Eigenvalue / Eigenvector Problem, Tech. Rep. UCB/CSD-97-971, UC Berkeley, Computer Science Division, May 1997.

12

J. DONGARRA, J. DU CROZ, S. HAMMARLING, J. WASNIEWSKI, AND A. ZEMA, A Proposal for a Fortran 90 Interface for LAPACK, Computer Science Dept. Technical Report CS-95-295, University of Tennessee, Knoxville, TN, 1995.
(Also LAPACK Working Note #101).

13

J. DONGARRA, W. OWCZARZ, J. WASNIEWSKI, AND P. YALAMOV, Testing Software for LAPACK90, Computer Science Dept. Technical Report CS-98-401, University of Tennessee, Knoxville, TN, 1998.
(Also LAPACK Working Note #138).

14

J. DONGARRA AND J. WASNIEWSKI, High Performance Linear Algebra Package - LAPACK90, Computer Science Dept. Technical Report CS-98-384, University of Tennessee, Knoxville, TN, 1998.
(Also LAPACK Working Note #134).

15

J. J. DONGARRA, J. DU CROZ, I. S. DUFF, AND S. HAMMARLING, A set of Level 3 Basic Linear Algebra Subprograms, ACM Trans. Math. Soft., 16 (1990), pp. 1-17.

16

J. J. DONGARRA, J. DU CROZ, S. HAMMARLING, AND R. J. HANSON, An extended set of FORTRAN basic linear algebra subroutines, ACM Trans. Math. Soft., 14 (1988), pp. 1-17.

17

J. J. DONGARRA, I. S. DUFF, D. SORENSEN, AND H. A. VAN DER VORST, Numerical Linear Algebra for High-Performance Computers, SIAM, Second ed., 1998.

18

J. J. DONGARRA AND E. GROSSE, Distribution of mathematical software via electronic mail, Communications of the ACM, 30 (1987), pp. 403-407.

19

F. GANTMACHER, The Theory of Matrices, vol. II (transl.), Chelsea, New York, 1959.

20

G. GOLUB AND C. F. VAN LOAN, Matrix Computations, Johns Hopkins University Press, Baltimore, MD, third ed., 1996.

21

N. J. HIGHAM, Accuracy and Stability of Numerical Algorithms, SIAM, 1996.

22

IBM, IBM Engineering and Scientific Subroutine Library for AIX, Version 3, Volume 1 ed., December 1997.
Pub. number SA22-7272-0.

23

height 2pt depth -1.6pt width 23pt, Engineering and Scientific Subroutine Library for AIX Guide and Reference.
http://www.rs6000.ibm.com/resource/aix_resource/sp_books/essl/index.html, 2000.

24

B. KåGSTRÖM, A Perturbation Analysis of the Generalized Sylvester Equation 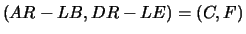$({AR - LB, DR - LE ) = (C, F})$, SIAM J. Matrix Anal. Appl., 15 (1994), pp. 1045-1060.

25

B. KåGSTRÖM AND P. POROMAA, Computing Eigenspaces with Specified Eigenvalues of a Regular Matrix Pair (A,B) and Condition Estimation: Theory, Algorithms and Software, Numerical Algorithms, 12 (1996), pp. 369-407.
Also Report # UMINF - 94.04 at Umeå University and LAPACK Working Note # 87.

26

height 2pt depth -1.6pt width 23pt, LAPACK-Style Algorithms and Software for Solving the Generalized Sylvester Equation and Estimating the Separation between Regular Matrix Pairs, ACM Trans. on Math. Software, 22 (1996), pp. 78-103.
Also Report # UMINF - 93.23 at Umeå University (Sweden) and LAPACK Working Note # 75.

27

B. KåGSTRÖM AND L. WESTIN, Generalized Schur Methods with Condition Estimators for Solving the Generalized Sylvester Equation, IEEE Transactions on Automatic Control, 34 (1989), pp. 745-751.

28

B. KÅGSTRÖM, A Direct Method for Reordering Eigenvalues in the Generalized Real Schur Form of a Regular Matrix Pair (A, B), in Linear Algebra for Large Scale and Real-Time Applications, M. S. Moonen et al., eds., Kluwer Academic Publ., 1993, pp. 195-218.

29

W. KAHAN, Accurate Eigenvalues of a Symmetric Tridiagonal Matrix, Tech. Rep. CS41, Stanford University, Computer Science Dept., July 1966.

30

C. L. LAWSON, R. J. HANSON, D. KINCAID, AND F. T. KROGH, Basic linear algebra subprograms for Fortran usage, ACM Trans. Math. Soft., 5 (1979), pp. 308-323.

31

M. METCALF AND J. REID, FORTRAN 90/95 Explained, Oxford University Press, Oxford, UK, second ed., 1996.

32

C. B. MOLER AND G. W. STEWART, An Algorithm for Generalized Matrix Eigenvalue Problems, SIAM J. Numer. Anal., 10 (1973), pp. 241-256.

33

C. PAIGE, Computing the generalized singular value decomposition, SIAM J. Sci. Stat., 7 (1986), pp. 1126-1146.

34

B. PARLETT AND F. V., Accurate Singular Values and Differential QD Algorithms, Tech. Rep. CPAM-554, University of California at Berkeley, Mathematics Department, July 1992.

35

G. QUINTANA-ORTI, E. QUINTANA-ORTI, AND A. PETITET, Efficient Solution of the Rank-Deficient Linear Least Squares Problem, SIAM Journal on Scientific and Statistical Computing, 20 (1999), pp. 1155-1163.
Also LAPACK Working Note # 113: http://www.netlib.org/lapack/lawns/lawn113.ps or http://www.netlib.org/lapack/lawns/lawn113.pdf.

36

G. QUINTANA-ORTI, X. SUN, AND C. H. BISCHOF, BLAS-3 Version of the QR Factorization with Column Pivoting.
http://www.netlib.org/lapack/lawns/lawn114.ps or http://www.netlib.org/lapack/lawnspdf/lawn114.pdf, 1996.
PRISM Working Note # 26 and LAPACK Working Note # 114.

37

B. T. SMITH, J. M. BOYLE, J. J. DONGARRA, B. S. GARBOW, Y. IKEBE, V. C. KLEMA, AND C. B. MOLER, Matrix Eigensystem Routines - EISPACK Guide, vol. 6 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 1976.

38

G. W. STEWART, On the sensitivity of the eigenvalue problem 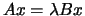$A x = \lambda B x$, SIAM J. Num. Anal., 9 (1972), pp. 669-686.

39

height 2pt depth -1.6pt width 23pt, Error and perturbation bounds for subspaces associated with certain eigenvalue problems, SIAM Review, 15 (1973), pp. 727-764.

40

G. W. STEWART AND J.-G. SUN, Matrix Perturbation Theory, Academic Press, New York, 1990.

41

SUN MICROSYSTEMS INC., Sun Performance Library User's Guide.
http://docs.sun.com/htmlcoll/coll.118.3/iso-8859-1/PERFLIBUG/plug_bookTOC.html.

42

R. C. WARD, Balancing the Generalized Eigenvalue Problem, SIAM J. Sci. Stat. Comp., 2 (1981), pp. 141-152.

43

R. C. WHALEY, A. PETITET, AND J. J. DONGARRA, Automated empirical optimization of software and the ATLAS project, To appear in Parallel Computing, (2001).
Also available as University of Tennessee LAPACK Working Note #147, UT-CS-00-448, 2000 (www.netlib.org/lapack/lawns/lawn147.ps).

44

J. H. WILKINSON, Kronecker's canonical form and the QZ algorithm, Lin. Alg. Appl., 28 (1979), pp. 285-303.