Table 2.3:
Driver routines for linear least squares problems
| Operation |
real/complex |
solve LLS using 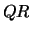 or or 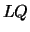 factorization factorization |
LA_GELS |
| solve LLS using complete orthogonal factorization |
LA_GELSY |
| solve LLS using SVD |
LA_GELSS |
| solve LLS using divide-and-conquer SVD |
LA_GELSD |