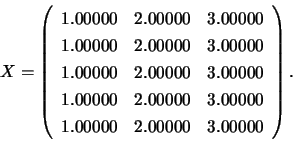Example (from Program LA_PTSVX_EXAMPLE)

The results below are computed with $\epsilon = 1.19209 \times 10^{-7}$.

Matrices $A$ and $B$ are the same as in Example for LA_PTSV.

The call:
CALL LA_PTSVX( D, E, B, X, FERR=FERR, BERR=BERR, RCOND=RCOND )

${\bf FERR, BERR}$ and ${\bf RCOND}$ on exit:

$$\begin{array}{c} {\bf FERR} \\ \begin{array}{\vert ccc\ve... ...line 1.18462 \times 10^{-1} \\ \hline \end{array} \end{array}$$

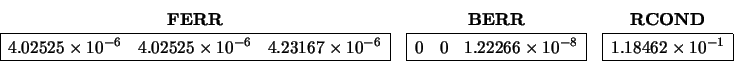
The forward and backward errors of the three solution vectors are:

$$\left( \begin{array}{ccc} 4.02525 \times 10^{-6} & 4.02525 ... ...ray}{ccc} 0 & 0 & 1.22266 \times 10^{-8} \end{array} \right).$$

The estimate of the reciprocal condition number of matrix $A$ is $1.18462 \times 10^{-1}$

The solution of the system $A\,X = B$ is:

$$X = \left( \begin{array}{rrr} 1.00000 & 2.00000 & 3.00000 ... ...3.00000 \\ 1.00000 & 2.00000 & 3.00000 \end{array} \right).$$