




Next: Triangular Linear Systems
Up: Computational Routines for Linear
Previous: Symmetric/Hermitian Positive Definite Linear
Contents
Index
LA_SYTRF / LA_HETRF
Real, complex, and complex Hermitian versions.
SUBROUTINE LA_SYTRF( UPLO, N, A, LDA, &
IPIV, WORK, LWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDA, LWORK, N
INTEGER, INTENT(OUT) :: INFO, IPIV(*)
type(wp), INTENT(INOUT) :: A( LDA,*)
type(wp), INTENT(OUT) :: WORK( LWORK )
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_SYTRF / LA_HETRF compute the factorization of
a real symmetric / complex symmetric / complex Hermitian matrix  using the Bunch-Kaufman diagonal pivoting method.
using the Bunch-Kaufman diagonal pivoting method.
References: See [1] and [9,21,20].
-----------------------------------
LA_SYTRS / LA_HETRS
Real, complex, and complex Hermitian versions.
SUBROUTINE LA_SYTRS( UPLO, N, NRHS, A, &
LDA, IPIV, B, LDB, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDA, LDB, N, NRHS
INTEGER, INTENT(OUT) :: INFO
INTEGER , INTENT(IN) :: IPIV(*)
type(wp), INTENT(IN) :: A( LDA,*)
type(wp), INTENT(INOUT) :: rhs
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
rhs ::= B(LDB,*)  B(*)
B(*)
LA_SYTRS / LA_HETRS solve a system of linear equations
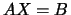 with a real symmetric / complex symmetric / complex
Hermitian matrix
with a real symmetric / complex symmetric / complex
Hermitian matrix  using the factorization
computed by LA_SYTRF / LA_HETRF, respectively.
using the factorization
computed by LA_SYTRF / LA_HETRF, respectively.
References: See [1] and [9,20].
-----------------------------------
LA_SYCON / LA_HECON
Real version.
SUBROUTINE LA_SYCON( UPLO, N, A, LDA, &
IPIV, ANORM, RCOND, WORK, IWORK, &
INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDA, N
INTEGER, INTENT(OUT) :: INFO, IWORK(*)
REAL(wp), INTENT(IN) :: ANORM
REAL(wp), INTENT(OUT) :: RCOND
INTEGER, INTENT(IN) :: IPIV(*)
REAL(wp), INTENT(IN) :: A( LDA,*)
REAL(wp), INTENT(OUT) :: WORK(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
Complex and complex Hermitian versions.
SUBROUTINE LA_SYCON / LA_HECON( UPLO, &
N, A, LDA, IPIV, ANORM, RCOND, WORK, &
INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDA, N
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(IN) :: ANORM
REAL(wp), INTENT(OUT) :: RCOND
INTEGER, INTENT(IN) :: IPIV(*)
COMPLEX(wp), INTENT(IN) :: A( LDA,*)
COMPLEX(wp), INTENT(OUT) :: WORK(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_SYCON / LA_HECON estimates the reciprocal of the condition
number of a real symmetric / complex symmetric / complex
Hermitian matrix  using the factorization computed by
LA_SYTRF / LA_HETRF, respectively.
using the factorization computed by
LA_SYTRF / LA_HETRF, respectively.
References: See [1] and [9,21,20].
-----------------------------------
LA_SYRFS / LA_HERFS
Real version.
SUBROUTINE LA_SYRFS( UPLO, N, NRHS, A, &
LDA, AF, LDAF, IPIV, B, LDB, X, LDX, &
FERR, BERR, WORK, IWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDA, LDAF, LDB, &
LDX, N, NRHS
INTEGER, INTENT(OUT) :: INFO, IWORK(*)
INTEGER, INTENT(IN) :: IPIV(*)
REAL(wp), INTENT(OUT) :: err
REAL(wp), INTENT(IN) :: A( LDA,*), &
AF( LDAF,*), rhs
REAL(wp), INTENT(INOUT) :: sol
REAL(wp), INTENT(OUT) :: WORK(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
rhs ::= B(LDB,*)  B(*)
B(*)
sol ::= X(LDX,*)  X(*)
X(*)
err ::= FERR(*), BERR(*)  FERR, BERR
FERR, BERR
Complex and complex Hermitian versions.
SUBROUTINE LA_SYRFS / LA_HERFS( UPLO, &
N, NRHS, A, LDA, AF, LDAF, IPIV, B, &
LDB, X, LDX, FERR, BERR, WORK, &
RWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDA, LDAF, LDB, &
LDX, N, NRHS
INTEGER, INTENT(OUT) :: INFO
INTEGER, INTENT(IN) :: IPIV(*)
REAL(wp), INTENT(OUT) :: err, RWORK(*)
COMPLEX(wp), INTENT(IN) :: A( LDA,*), &
AF( LDAF,*), rhs
COMPLEX(wp), INTENT(INOUT) :: sol
COMPLEX(wp), INTENT(OUT) :: WORK(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
rhs ::= B(LDB,*)  B(*)
B(*)
sol ::= X(LDX,*)  X(*)
X(*)
err ::= FERR(*), BERR(*)  FERR, BERR
FERR, BERR
LA_SYRFS / LA_HERFS improve the computed solution to a system
of linear equations when the coefficient matrix is real symmetric / complex
symmetric / complex Hermitian indefinite, and provides error bounds
and backward error estimates for the solution.
References: See [1] and [9,21,20].
-----------------------------------
LA_SYTRI / LA_HETRI
Real, complex, and complex Hermitian versions.
SUBROUTINE LA_SYTRI /LA_HETRI( UPLO, &
N, A, LDA, IPIV, WORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDA, N
INTEGER, INTENT(OUT) :: INFO
INTEGER, INTENT(IN) :: IPIV(*)
type(wp), INTENT(INOUT) :: A( LDA,*)
type(wp), INTENT(OUT) :: WORK(*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_SYTRI / LA_HETRI compute the inverse of real symmetric,
complex symmetric / complex Hermitian indefinite matrix  using the
factorization computed by LA_SYTRF / LA_HETRF respectively.
using the
factorization computed by LA_SYTRF / LA_HETRF respectively.
References: See [1] and [9,20].
-----------------------------------
LA_SPTRF / LA_HPTRF
Real, complex, and complex Hermitian versions.
SUBROUTINE LA_SPTRF /LA_HPTRF( UPLO, &
N, AP, IPIV, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: N
INTEGER, INTENT(OUT) :: INFO, IPIV(*)
type(wp), INTENT(INOUT) :: AP(*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_SPTRF and LA_HPTRF compute the factorization of a real
symmetric / complex symmetric / complex Hermitian indefinite matrix  stored in packed format using the Bunch-Kaufman diagonal pivoting method.
stored in packed format using the Bunch-Kaufman diagonal pivoting method.
References: See [1] and [9,21,20].
-----------------------------------
LA_SPTRS / LA_HPTRS
Real, complex, and complex Hermitian versions.
SUBROUTINE LA_SPTRS /LA_HPTRS( UPLO, &
N, NRHS, AP, IPIV, B, LDB, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDB, N, NRHS
INTEGER, INTENT(OUT) :: INFO
INTEGER, INTENT(IN) :: IPIV(*)
type(wp), INTENT(IN) :: AP(*)
type(wp), INTENT(INOUT) :: B(LDB,*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
rhs ::= B(LDB,*)  B(*)
B(*)
LA_SPTRS / LA_HPTRS solve a system of linear equations 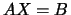 with a real symmetric / complex symmetric / complex Hermitian matrix
with a real symmetric / complex symmetric / complex Hermitian matrix  stored in packed format using the factorization computed by LA_SPTRF /
LA_HPTRF respectively.
stored in packed format using the factorization computed by LA_SPTRF /
LA_HPTRF respectively.
References: See [1] and [9,20].
-----------------------------------
LA_SPCON / LA_HPCON
Real version.
SUBROUTINE LA_SPCON( UPLO, N, AP, IPIV, &
ANORM, RCOND, WORK, IWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: N
INTEGER, INTENT(OUT) :: INFO, IWORK(*)
REAL(wp), INTENT(IN) :: ANORM
REAL(wp), INTENT(OUT) :: RCOND
INTEGER, INTENT(IN) :: IPIV( * )
REAL(wp), INTENT(IN) :: AP(*)
REAL(wp), INTENT(OUT) :: WORK(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
Complex and complex Hermitian versions.
SUBROUTINE LA_SPCON /LA_HPCON( UPLO, &
N, AP, IPIV, ANORM, RCOND, WORK, &
INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: N
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(IN) :: ANORM
REAL(wp), INTENT(OUT) :: RCOND
INTEGER, INTENT(IN) :: IPIV( * )
COMPLEX(wp), INTENT(IN) :: AP(*)
COMPLEX(wp), INTENT(OUT) :: WORK(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_SPCON / LA_HPCON estimates the reciprocal of the condition number
of real symmetric / complex symmetric / complex Hermitian indefinite packed matrix  using the factorization computed by LA_SPTRF /
LA_HPTRF respectively.
using the factorization computed by LA_SPTRF /
LA_HPTRF respectively.
References: See [1] and [9,20,21].
-----------------------------------
LA_SPRFS / LA_HPRFS
Real version.
SUBROUTINE LA_SPRFS( UPLO, N, NRHS, &
AP, AFP, IPIV, B, LDB, X, LDX, FERR, &
BERR, WORK, IWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDB, LDX, N, NRHS
INTEGER, INTENT(OUT) :: INFO, IWORK(*)
INTEGER, INTENT(IN) :: IPIV(*)
REAL(wp), INTENT(OUT) :: err
REAL(wp), INTENT(IN) :: AFP(*), AP(*), rhs
REAL(wp), INTENT(INOUT) :: sol
REAL(wp), INTENT(OUT) :: WORK(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
rhs ::= B(LDB,*)  B(*)
B(*)
sol ::= X(LDX,*)  X(*)
X(*)
err ::= FERR(*), BERR(*)  FERR, BERR
FERR, BERR
Complex and complex Hermitian versions.
SUBROUTINE LA_SPRFS /LA_HPRFS( UPLO, &
N, NRHS, AP, AFP, IPIV, B, LDB, X, LDX, &
FERR, BERR, WORK, RWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDB, LDX, N, NRHS
INTEGER, INTENT(OUT) :: INFO
INTEGER, INTENT(IN) :: IPIV(*)
REAL(wp), INTENT(OUT) :: err, RWORK(*)
COMPLEX(wp), INTENT(IN) :: AFP(*), AP(*), &
rhs
COMPLEX(wp), INTENT(INOUT) :: sol
COMPLEX(wp), INTENT(OUT) :: WORK(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
rhs ::= B(LDB,*)  B(*)
B(*)
sol ::= X(LDX,*)  X(*)
X(*)
err ::= FERR(*), BERR(*)  FERR, BERR
FERR, BERR
LA_SPRFS / LA_HPRFS improve the computed solution to a system
of linear equations when the coefficient matrix is a real symmetric / complex
symmetric / complex Hermitian, indefinite and packed, and provides
error bounds and backward error estimates for the solution.
References: See [1] and [9,21,20].
-----------------------------------
LA_SPTRI / LA_HPTRI
Real, complex, and complex Hermitian versions.
SUBROUTINE LA_SYTRI /LA_HETRI( UPLO, &
N, AP, IPIV, WORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: N
INTEGER, INTENT(OUT) :: INFO
INTEGER, INTENT(IN) :: IPIV(*)
type(wp), INTENT(INOUT) :: AP(*)
type(wp), INTENT(OUT) :: WORK(*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_SPTRI / LA_HPTRI compute the inverse of a real symmetric
/ complex symmetric / complex Hermitian, indefinite matrix  in packed storage
using the factorization computed by LA_SPTRF / LA_HPTRF respectively.
in packed storage
using the factorization computed by LA_SPTRF / LA_HPTRF respectively.
References: See [1] and [9,20].
-----------------------------------





Next: Triangular Linear Systems
Up: Computational Routines for Linear
Previous: Symmetric/Hermitian Positive Definite Linear
Contents
Index
Susan Blackford
2001-08-19