




Next: Computational Routines for the
Up: Computational Routines
Previous: Computational Routines for Orthogonal
Contents
Index
Computational Routines for the Symmetric Eigenproblem
LA_SYTRD / LA_HETRD
Real and complex versions.
SUBROUTINE LA_SYTRD / LA_HETRD( UPLO, &
N, A, LDA, D, E, TAU, WORK, LWORK, &
INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDA, LWORK, N
INTEGER, INTENT(OUT) :: INFO
type(wp), INTENT(INOUT) :: A(LDA,*)
REAL(wp), INTENT(OUT) :: D(*), E(*)
type(wp), INTENT(OUT) :: TAU(*), &
WORK(LWORK)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_SYTRD / LA_HETRD reduces a real symmetric / complex Hermitian
matrix  to real symmetric tridiagonal form
to real symmetric tridiagonal form 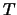 by an orthogonal
/ unitary similarity transformation:
by an orthogonal
/ unitary similarity transformation: 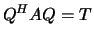 .
.
References: See [1] and [9,20].
-----------------------------------
LA_SPTRD / LA_HPTRD
Real and complex versions.
SUBROUTINE LA_SPTRD / LA_HPTRD( UPLO, &
N, AP, D, E, TAU, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: N
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(OUT) :: D(*), E(*)
type(wp), INTENT(INOUT) :: AP(*)
type(wp), INTENT(OUT) :: TAU(*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_SPTRD / LA_HPTRD reduces a real symmetric / complex Hermitian
matrix  stored in packed storage to real symmetric tridiagonal form
stored in packed storage to real symmetric tridiagonal form 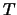 by
an orthogonal / unitary similarity transformation:
by
an orthogonal / unitary similarity transformation: 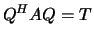 .
.
References: See [1] and [9,20].
-----------------------------------
LA_SBTRD / LA_HBTRD
Real and complex versions.
SUBROUTINE LA_SBTRD / LA_HBTRD( VECT, &
UPLO, N, KD, AB, LDAB, D, E, Q, LDQ, &
WORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO, &
VECT
INTEGER, INTENT(IN) :: KD, LDAB, LDQ, N
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(OUT) :: D(*), E(*)
type(wp), INTENT(INOUT) :: AB(LDAB,*), &
Q(LDQ,*)
type(wp), INTENT(OUT) :: WORK(*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_SBTRD / LA_HBTRD reduces a real symmetric / complex Hermitian
band matrix  to real symmetric tridiagonal form
to real symmetric tridiagonal form 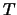 by
an orthogonal / unitary similarity transformation:
by
an orthogonal / unitary similarity transformation: 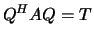 .
.
References: See [1] and [9,20].
-----------------------------------
LA_ORGTR / LA_UNGTR
Real and complex versions.
SUBROUTINE LA_ORGTR / LA_UNGTR( UPLO, &
N, A, LDA, TAU, WORK, LWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDA, LWORK, N
INTEGER, INTENT(OUT) :: INFO
type(wp), INTENT(IN) :: TAU(*)
type(wp), INTENT(INOUT) :: A(LDA,*)
type(wp), INTENT(OUT) :: WORK(LWORK)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_ORGTR / LA_UNGTR generates a real orthogonal
/ complex unitary
matrix 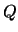 which is defined as the product of
which is defined as the product of 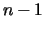 elementary reflectors
of order
elementary reflectors
of order 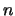 , as returned by LA_SYTRD / LA_HETRD.
, as returned by LA_SYTRD / LA_HETRD.
References: See [1] and [9,20].
-----------------------------------
LA_ORMTR / LA_UNMTR
Real and complex versions.
SUBROUTINE LA_ORMTR / LA_UNMTR( SIDE, &
UPLO, TRANS, M, N, A, LDA, TAU, C, LDC, &
WORK, LWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: SIDE, &
TRANS, UPLO
INTEGER, INTENT(IN) :: LDA, LDC, &
LWORK, M, N
INTEGER, INTENT(OUT) :: INFO
type(wp), INTENT(IN) :: A(LDA,*), TAU(*)
type(wp), INTENT(OUT) :: WORK(LWORK)
type(wp), INTENT(INOUT) :: C(LDC,*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_ORMTR / LA_UNMTR
overwrite the general real / complex 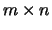 matrix
matrix 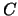 with
a real orthogonal / complex unitary matrix
with
a real orthogonal / complex unitary matrix 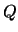 of order
of order 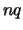 .
.
References: See [1] and [9,20].
-----------------------------------
LA_OPGTR / LA_UPGTR
Real and complex versions.
SUBROUTINE LA_OPGTR / LA_UPGTR( UPLO, &
N, AP, TAU, Q, LDQ, WORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDQ, N
INTEGER, INTENT(OUT) :: INFO
type(wp), INTENT(IN) :: AP(*), TAU(*)
type(wp), INTENT(OUT) :: Q(LDQ,*), WORK(*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_OPGTR / LA_UPGTR
generate a real orthogonal / complex unitary matrix 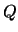 which is defined as the
product of
which is defined as the
product of 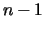 elementary reflectors
elementary reflectors 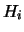 of order
of order 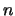 , as returned by
LA_SPTRD / LA_HPTRD using packed storage.
, as returned by
LA_SPTRD / LA_HPTRD using packed storage.
References: See [1] and [9,20].
-----------------------------------
LA_OPMTR / LA_UPMTR
Real and complex versions.
SUBROUTINE LA_OPMTR / LA_UPMTR( SIDE, &
UPLO, TRANS, M, N, AP, TAU, C, LDC, &
WORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: SIDE, &
TRANS, UPLO
INTEGER, INTENT(IN) :: LDC, M, N
INTEGER, INTENT(OUT) :: INFO
type(wp), INTENT(IN) :: AP(*), TAU(*)
type(wp), INTENT(INOUT) :: C(LDC,*)
type(wp), INTENT(OUT) :: WORK(*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_OPMTR / LA_UPMTR
overwrite the general real / complex 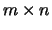 matrix
matrix 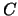 with
a real orthogonal / complex unitary matrix
with
a real orthogonal / complex unitary matrix 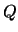 of order
of order 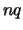 ,
defined as the product of
,
defined as the product of  elementary reflectors, as returned by LA_SPTRD / LA_HPTRD.
elementary reflectors, as returned by LA_SPTRD / LA_HPTRD.
References: See [1] and [9,20].
-----------------------------------
LA_STEQR
Real and complex versions.
SUBROUTINE LA_STEQR( COMPZ, N, D, E, Z, &
LDZ, WORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: COMPZ
INTEGER, INTENT(IN) :: LDZ, N
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(INOUT) :: D(*), E(*)
REAL(wp), INTENT(OUT) :: WORK(*)
type(wp), INTENT(INOUT) :: Z(LDZ,*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_STEQR
computes all eigenvalues and, optionally, eigenvectors of a
symmetric tridiagonal matrix using the implicit 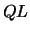 or
or 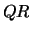 method.
method.
References: See [1] and [9,20].
-----------------------------------
LA_STERF
Real version.
SUBROUTINE LA_STERF( N, D, E, INFO )
INTEGER, INTENT(IN) :: N
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(INOUT) :: D(*), E(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_STERF
computes all eigenvalues of a symmetric tridiagonal matrix
using the Pal-Walker-Kahan variant of the 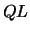 or
or 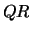 algorithm.
algorithm.
References: See [1] and [9,20].
-----------------------------------
LA_STEDC
Real version.
SUBROUTINE LA_STEDC( COMPZ, N, D, E, Z, &
LDZ, WORK, LWORK, IWORK, LIWORK, &
INFO )
CHARACTER(LEN=1), INTENT(IN) :: COMPZ
INTEGER, INTENT(IN) :: LDZ, LIWORK, &
LWORK, N
INTEGER, INTENT(OUT) :: INFO, &
IWORK(LIWORK)
REAL(wp), INTENT(INOUT) :: D(*), E(*)
REAL(wp), INTENT(INOUT) :: Z(LDZ,*)
REAL(wp), INTENT(OUT) :: WORK(LWORK)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
Complex version.
SUBROUTINE LA_STEDC( COMPZ, N, D, E, Z, &
LDZ, WORK, LWORK, RWORK, LRWORK, &
IWORK, LIWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: COMPZ
INTEGER, INTENT(IN) :: LDZ, LIWORK, &
LRWORK, LWORK, N
INTEGER, INTENT(OUT) :: INFO, &
IWORK(LIWORK)
REAL(wp), INTENT(INOUT) :: D(*), E(*)
REAL(wp), INTENT(OUT) :: RWORK(LRWORK)
COMPLEX(wp), INTENT(INOUT) :: Z(LDZ,*)
COMPLEX(wp), INTENT(OUT) :: &
WORK(LWORK)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_STEDC
computes all eigenvalues and, optionally, eigenvectors of a
symmetric tridiagonal matrix using the divide and conquer method.
References: See [1] and [9,20].
-----------------------------------
LA_STEGR
Real and complex versions.
SUBROUTINE LA_STEGR( JOBZ, RANGE, N, &
D, E, VL, VU, IL, IU, ABSTOL, M, W, Z, &
LDZ, ISUPPZ, WORK, LWORK, &
IWORK, LIWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: JOBZ, &
RANGE
INTEGER, INTENT(IN) :: IL, IU, LDZ, &
LIWORK, LWORK, N
INTEGER, INTENT(OUT) :: INFO, M
INTEGER, INTENT(OUT) :: ISUPPZ( * ), &
IWORK(LIWORK)
REAL(wp), INTENT(IN) :: ABSTOL, VL, VU
REAL(wp), INTENT(INOUT) :: D( * ), E( * )
REAL(wp), INTENT(IN) :: W( * )
REAL(wp), INTENT(OUT) :: WORK(LWORK)
type(wp), INTENT(OUT) :: Z( LDZ, * )
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_STEGR
computes selected eigenvalues and, optionally, eigenvectors
of a real symmetric / complex Hermitian tridiagonal matrix 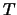 .
.
References: See [1] and [9,20,11].
-----------------------------------
LA_STEBZ
Real version.
SUBROUTINE LA_STEBZ( RANGE, ORDER, &
N, VL, VU, IL, IU, ABSTOL, D, E, M, &
NSPLIT, W, IBLOCK, ISPLIT, WORK, &
IWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: &
ORDER, RANGE
INTEGER, INTENT(IN) :: IL, IU, M, N
INTEGER, INTENT(OUT) :: INFO, NSPLIT, &
IBLOCK(*), ISPLIT(*), IWORK(*)
REAL(wp), INTENT(IN) :: ABSTOL, VL, VU, &
D(*), E(*)
REAL(wp), INTENT(OUT) :: W(*), WORK(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_STEBZ
computes the eigenvalues of a symmetric tridiagonal
matrix 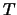 . The user may ask for all eigenvalues
in the half-open interval (
. The user may ask for all eigenvalues
in the half-open interval (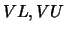 ], or the
], or the 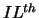 through
through 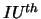 eigenvalues.
eigenvalues.
References: See [1] and [9,20,29].
-----------------------------------
LA_STEIN
Real and complex versions.
SUBROUTINE LA_STEIN( N, D, E, M, W, &
IBLOCK, ISPLIT, Z, LDZ, WORK, IWORK, &
IFAIL, INFO )
INTEGER, INTENT(IN) :: LDZ, M, N, &
IBLOCK(*), ISPLIT(*)
INTEGER, INTENT(OUT) :: INFO, IFAIL(*), &
IWORK(*)
REAL(wp), INTENT(IN) :: D(*), E(*), W(*)
REAL(wp), INTENT(OUT) :: WORK(*)
type(wp), INTENT(OUT) :: Z( LDZ, * )
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_STEIN
computes the eigenvectors of a real symmetric tridiagonal
matrix 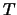 corresponding to specified eigenvalues, using inverse
iteration.
corresponding to specified eigenvalues, using inverse
iteration.
References: See [1] and [9,20].
-----------------------------------
LA_PTEQR
Real and complex versions.
SUBROUTINE LA_PTEQR( COMPZ, N, D, E, Z, &
LDZ, WORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: COMPZ
INTEGER, INTENT(IN) :: INFO, LDZ, N
REAL(wp), INTENT(INOUT) :: D(*), E(*)
REAL(wp), INTENT(OUT) :: WORK(*)
type(wp), INTENT(INOUT) :: Z(LDZ,*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_PTEQR
computes all eigenvalues and, optionally, eigenvectors of a
symmetric positive definite tridiagonal matrix by first factoring the
matrix using LA_PTTRF and then calling LA_BDSQR to
compute the singular values of the bidiagonal factor.
References: See [1] and [9,20].
-----------------------------------





Next: Computational Routines for the
Up: Computational Routines
Previous: Computational Routines for Orthogonal
Contents
Index
Susan Blackford
2001-08-19