




Next: Example (from Program LA_GGESX_EXAMPLE)
Up: Generalized Nonsymmetric Eigenvalue Problems
Previous: Purpose
Contents
Index
- A
- (input/output) REAL or COMPLEX
square array, shape
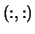 .
.
On entry, the matrix  .
.
On exit, the matrix 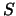 .
.
- B
- (input/output) REAL or COMPLEX
square array, shape
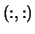 with
with
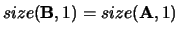 .
.
On entry, the matrix 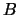 .
.
On exit, the matrix 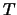 .
.
- alpha
- (output) REAL or COMPLEX array,
shape
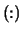 with
with
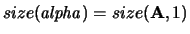 .
.
The values of 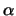 .
.
 ::= ALPHAR(:), ALPHAI(:)
::= ALPHAR(:), ALPHAI(:)  ALPHA(:),
ALPHA(:),
where
ALPHAR(:), ALPHAI(:) are of
REAL type (for the real and imaginary parts)
and ALPHA(:) is of COMPLEX type.
- BETA
- (output) REAL or COMPLEX
array, shape
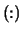 with
with
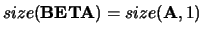 .
.
The values of 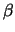 .
.
Note: The generalized eigenvalues of the pair 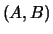 are the scalars
are the scalars
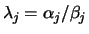 . These quotients may
easily over- or underflow, and
. These quotients may
easily over- or underflow, and 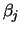 may even
be zero. Thus, the user should avoid computing them naively.
may even
be zero. Thus, the user should avoid computing them naively.
Note: If A and B are real then complex eigenvalues
occur in complex conjugate pairs. Each pair is stored
consecutively. Thus a complex conjugate pair is given by
where
- VSL
- Optional (output) REAL or
COMPLEX square array, shape
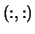 with
with
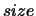 (VSL,1)
(VSL,1) 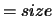 (A,1).
(A,1).
The left Schur vectors.
- VSR
- Optional (output) REAL or
COMPLEX square array, shape
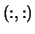 with
with
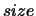 (VSR,1)
(VSR,1) 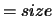 (A,1).
(A,1).
The right Schur vectors.
- SELECT
- Optional (input) LOGICAL FUNCTION
- LOGICAL FUNCTION SELECT( alpha
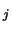 , BETA
, BETA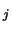 )
)
type(wp), INTENT(IN) ::
alpha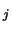 , BETA
, BETA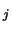
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
alpha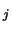 ::= ALPHAR
::= ALPHAR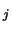 , ALPHAI
, ALPHAI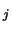
 ALPHA
ALPHA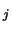

Note: Select must be present if SDIM, RCONDE and RCONDF
are desired.
- SDIM
- Optional (output) INTEGER.
The number of eigenvalues (after sorting) for which SELECT 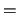 .TRUE.
(If
.TRUE.
(If  and
and 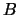 are real, complex conjugate pairs for which SELECT
are real, complex conjugate pairs for which SELECT 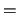 .TRUE. for either eigenvalue count as 2).
.TRUE. for either eigenvalue count as 2).
- RCONDE
- Optional (output) REAL array, shape
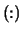 with
with 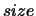 (RCONDE)
(RCONDE) 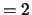 .
.
The reciprocal condition numbers for the average of the selected eigenvalues.
- RCONDV
- Optional (output) REAL array, shape
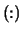 with
with
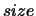 (RCONDV)
(RCONDV) 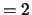 .
.
The reciprocal condition numbers
for the left and right deflating subspaces
corresponding to the selected eigenvalues.
- INFO
- Optional (output) INTEGER.
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INF...
...scaling.
\item[{$=$\ n+3:}] the reordering failed.
\end{infoarg} \end{infoarg}](img901.gif)
If INFO is not present and an error occurs, then
the program is terminated with an error message.
References: [1]
and [17,9,20,21].





Next: Example (from Program LA_GGESX_EXAMPLE)
Up: Generalized Nonsymmetric Eigenvalue Problems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19

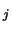 , BETA
, BETA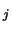 )
)
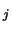 , BETA
, BETA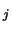
 COMPLEX
COMPLEX
 KIND(1.0D0)
KIND(1.0D0)
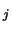 ::= ALPHAR
::= ALPHAR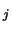 , ALPHAI
, ALPHAI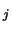
 ALPHA
ALPHA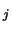

![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INF...
...scaling.
\item[{$=$\ n+3:}] the reordering failed.
\end{infoarg} \end{infoarg}](img901.gif)