




Next: Arguments
Up: Generalized Nonsymmetric Eigenvalue Problems
Previous: LA_GGESX
Contents
Index
LA_GGESX computes
for a pair of 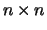 real or complex matrices
real or complex matrices 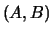 the
(generalized) real or complex Schur form, the generalized
eigenvalues in the form of scalar pairs
the
(generalized) real or complex Schur form, the generalized
eigenvalues in the form of scalar pairs
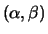 , and, optionally, the left and/or right Schur
vectors.
, and, optionally, the left and/or right Schur
vectors.
If  and
and 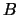 are real then the real-Schur form is computed,
otherwise the complex-Schur form is computed. The real-Schur form is a
pair of real matrices
are real then the real-Schur form is computed,
otherwise the complex-Schur form is computed. The real-Schur form is a
pair of real matrices 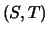 such that 1)
such that 1)
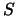 has block upper triangular form, with
has block upper triangular form, with 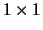 and
and
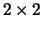 blocks along the main diagonal,
2)
blocks along the main diagonal,
2) 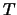 has upper triangular form with nonnegative
elements
on the main diagonal, and 3)
has upper triangular form with nonnegative
elements
on the main diagonal, and 3) 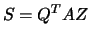 and
and
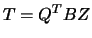 , where
, where 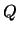 and
and 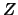 are orthogonal
matrices. The
are orthogonal
matrices. The 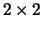 blocks of
blocks of 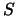 are ``standardized''
by making the corresponding elements of
are ``standardized''
by making the corresponding elements of 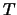 have the form
have the form
![\begin{displaymath}\left[ \begin{array}{cc}
a & 0 \\ 0 & b \end{array} \right] \end{displaymath}](img891.gif)
The complex-Schur form is a pair
of matrices 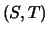 such that 1)
such that 1) 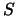 has
upper triangular form, 2)
has
upper triangular form, 2) 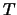 has upper triangular form
with nonnegative elements on the main diagonal, and 3)
has upper triangular form
with nonnegative elements on the main diagonal, and 3) 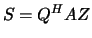 and
and
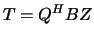 , where
, where 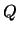 and
and 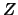 are unitary matrices.
are unitary matrices.
In both cases the columns of 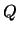 and
and 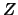 are called, respectively,
the left and right Schur vectors.
are called, respectively,
the left and right Schur vectors.
A generalized eigenvalue of the pair 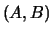 is, roughly
speaking, a scalar
of the form
is, roughly
speaking, a scalar
of the form
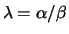 such that the matrix
such that the matrix
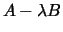 is singular. It is usually represented as the pair
is singular. It is usually represented as the pair
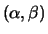 , as there
is a reasonable interpretation of the case
, as there
is a reasonable interpretation of the case 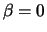 (even if
(even if
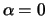 )
)
LA_GGESX also computes two
reciprocal condition numbers for the average of the selected
eigenvalues and reciprocal condition numbers for
the right and left deflating subspaces corresponding to the selected
eigenvalues.





Next: Arguments
Up: Generalized Nonsymmetric Eigenvalue Problems
Previous: LA_GGESX
Contents
Index
Susan Blackford
2001-08-19
![]() real or complex matrices
real or complex matrices ![]() the
(generalized) real or complex Schur form, the generalized
eigenvalues in the form of scalar pairs
the
(generalized) real or complex Schur form, the generalized
eigenvalues in the form of scalar pairs
![]() , and, optionally, the left and/or right Schur
vectors.
, and, optionally, the left and/or right Schur
vectors.
![]() and
and ![]() are real then the real-Schur form is computed,
otherwise the complex-Schur form is computed. The real-Schur form is a
pair of real matrices
are real then the real-Schur form is computed,
otherwise the complex-Schur form is computed. The real-Schur form is a
pair of real matrices ![]() such that 1)
such that 1)
![]() has block upper triangular form, with
has block upper triangular form, with ![]() and
and
![]() blocks along the main diagonal,
2)
blocks along the main diagonal,
2) ![]() has upper triangular form with nonnegative
elements
on the main diagonal, and 3)
has upper triangular form with nonnegative
elements
on the main diagonal, and 3) ![]() and
and
![]() , where
, where ![]() and
and ![]() are orthogonal
matrices. The
are orthogonal
matrices. The ![]() blocks of
blocks of ![]() are ``standardized''
by making the corresponding elements of
are ``standardized''
by making the corresponding elements of ![]() have the form
have the form
![\begin{displaymath}\left[ \begin{array}{cc}
a & 0 \\ 0 & b \end{array} \right] \end{displaymath}](img891.gif)