




Next: Computational Routines for the
Up: Computational Routines
Previous: Computational Routines for the
Contents
Index
Computational Routines for the Singular Value Decomposition
LA_GEBRD
Real and complex versions.
SUBROUTINE LA_GEBRD( M, N, A, LDA, D, E, &
TAUQ, TAUP, WORK, LWORK, INFO )
INTEGER, INTENT(IN) :: LDA, LWORK, M, N
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(OUT) :: D(*), E(*)
type(wp), INTENT(INOUT) :: A(LDA,*)
type(wp), INTENT(OUT) :: TAUP(*), TAUQ(*), &
WORK(LWORK)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_GEBRD
reduces a general real / complex 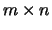 matrix
matrix  to upper or lower
bidiagonal form
to upper or lower
bidiagonal form 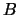 by an orthogonal / unitary transformation:
by an orthogonal / unitary transformation: 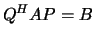 .
.
References: See [1] and [9,20].
-----------------------------------
LA_GBBRD
Real version.
SUBROUTINE LA_GBBRD( VECT, M, N, NCC, &
KL, KU, AB, LDAB, D, E, Q, LDQ, PT, &
LDPT, C, LDC, WORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: VECT
INTEGER, INTENT(IN) :: KL, KU, LDAB, &
LDC, LDPT, LDQ, M, N, NCC
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(OUT) :: D(*), E(*)
REAL(wp), INTENT(INOUT) :: AB(LDAB,*), &
C(LDC,*)
REAL(wp), INTENT(OUT) :: PT(LDPT,*), &
Q(LDQ,*), WORK(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
Complex version.
SUBROUTINE LA_GBBRD( VECT, M, N, NCC, &
KL, KU, AB, LDAB, D, E, Q, LDQ, PT, &
LDPT, C, LDC, WORK, RWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: VECT
INTEGER, INTENT(IN) :: KL, KU, LDAB, &
LDC, LDPT, LDQ, M, N, NCC
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(OUT) :: D(*), E(*),&
RWORK(*)
COMPLEX(wp), INTENT(INOUT) :: &
AB(LDAB,*), C(LDC,*)
COMPLEX(wp), INTENT(OUT) :: PT(LDPT,*), &
Q(LDQ,*), WORK(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_GBBRD
reduces a real / complex general 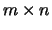 band matrix
band matrix  to real upper
bidiagonal form
to real upper
bidiagonal form 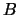 by an orthogonal / unitary transformation:
by an orthogonal / unitary transformation: 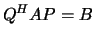 .
.
References: See [1] and [9,20].
-----------------------------------
LA_ORGBR / LA_UNGBR
Real and complex versions.
SUBROUTINE LA_ORGBR / LA_UNGBR( &
VECT, M, N, K, A, LDA, TAU, WORK, &
LWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: VECT
INTEGER, INTENT(IN) :: K, LDA, LWORK, M, &
N
INTEGER, INTENT(OUT) :: INFO
type(wp), INTENT(IN) :: TAU(*)
type(wp), INTENT(INOUT) :: A(LDA,*)
type(wp), INTENT(OUT) :: WORK(LWORK)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_ORGBR / LA_UNGBR
generates one of the real / complex orthogonal / unitary matrices 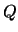 or
or  determined by LA_GEBRD when reducing a complex matrix
determined by LA_GEBRD when reducing a complex matrix  to bidiagonal
form:
to bidiagonal
form: 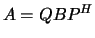 .
. 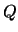 and
and  are defined as products of
elementary reflectors
are defined as products of
elementary reflectors 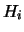 or
or 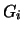 respectively.
respectively.
References: See [1] and [9,20].
-----------------------------------
LA_ORMBR / LA_UNMBR
Real and complex versions.
SUBROUTINE LA_ORMBR / LA_UNMBR( &
VECT, SIDE, TRANS, M, N, K, A, LDA, &
TAU, C, LDC, WORK, LWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: SIDE, &
TRANS, VECT
INTEGER, INTENT(IN) :: K, LDA, LDC, &
LWORK, M, N
INTEGER, INTENT(OUT) :: INFO
type(wp), INTENT(IN) :: A(LDA,*), TAU(*)
type(wp), INTENT(INOUT) :: C(LDA,*)
type(wp), INTENT(OUT) :: WORK(LWORK)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_ORMBR / LA_UNMBR
overwrites the general real / complex 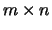 matrix
matrix 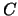 with the products
with the products 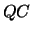 ,
,  ,
, 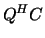 ,
, 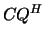 ,
,
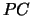 ,
, 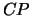 ,
, 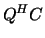 or
or 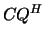 , respectively, where
, respectively, where 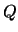 and
and  are the
orthogonal / unitary matrices determined by
LA_GEBRD when reducing a real / complex matrix
are the
orthogonal / unitary matrices determined by
LA_GEBRD when reducing a real / complex matrix  to
bidiagonal form:
to
bidiagonal form: 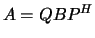 .
.
References: See [1] and [9,20].
-----------------------------------
LA_BDSQR
Real and complex versions.
SUBROUTINE LA_BDSQR( UPLO, N, NCVT, &
NRU, NCC, D, E, VT, LDVT, U, LDU, C, &
LDC, RWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: UPLO
INTEGER, INTENT(IN) :: LDC, LDU, LDVT, &
N, NCC, NCVT, NRU
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(INOUT) :: D(*), E(*)
REAL(wp), INTENT(OUT) :: RWORK(*)
type(wp), INTENT(INOUT) :: C(LDC,*), &
U(LDU,*), VT(LDVT,*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_BDSQR
computes the singular value decomposition (SVD) of a real
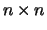 (upper or lower) bidiagonal matrix
(upper or lower) bidiagonal matrix 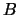 :
: 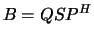 where
where 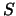 is a diagonal matrix with
non-negative diagonal elements (the singular values of
is a diagonal matrix with
non-negative diagonal elements (the singular values of 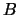 ), and
), and 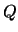 and
and 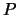 are orthogonal matrices.
are orthogonal matrices.
References: See [1] and [9,20,8,34].
-----------------------------------
LA_BDSDC
Real version.
SUBROUTINE LA_BDSDC( UPLO, COMPQ, N, &
D, E, U, LDU, VT, LDVT, Q, IQ, WORK, &
IWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: &
COMPQ, UPLO
INTEGER, INTENT(IN) :: LDU, LDVT, N
INTEGER, INTENT(OUT) :: INFO, IQ( * ), &
IWORK( * )
REAL(wp), INTENT(INOUT) :: D( * ), E( * )
REAL(wp), INTENT(OUT) :: Q(*), U(LDU,*), &
VT(LDVT,*), WORK(*)
where
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_BDSDC
computes the singular value decomposition (SVD) of a real
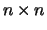 (upper or lower) bidiagonal matrix
(upper or lower) bidiagonal matrix 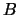 :
: 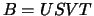 ,
using a divide and conquer method, where
,
using a divide and conquer method, where 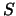 is a diagonal matrix
with non-negative diagonal elements (the singular values of
is a diagonal matrix
with non-negative diagonal elements (the singular values of 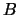 ), and
), and
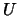 and
and 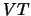 are orthogonal matrices of left and right singular vectors,
respectively. LA_BDSDC can be used to compute all singular values,
and optionally, singular vectors or singular vectors in compact form.
are orthogonal matrices of left and right singular vectors,
respectively. LA_BDSDC can be used to compute all singular values,
and optionally, singular vectors or singular vectors in compact form.
References: See [1] and [9,20].
-----------------------------------





Next: Computational Routines for the
Up: Computational Routines
Previous: Computational Routines for the
Contents
Index
Susan Blackford
2001-08-19