




Next: Arguments
Up: Symmetric Indefinite Linear Systems
Previous: LA_SYSV / LA_HESV
Contents
Index
LA_SYSV computes the solution to a linear system of
equations 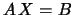 , where
, where  is a real or complex symmetric
matrix and
is a real or complex symmetric
matrix and 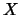 and
and 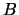 are rectangular matrices or vectors.
A diagonal pivoting method is used to factor
are rectangular matrices or vectors.
A diagonal pivoting method is used to factor  as
as
where 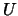 (or
(or 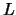 ) is a product of permutation
and unit upper (or lower) triangular matrices,
and
) is a product of permutation
and unit upper (or lower) triangular matrices,
and  is a symmetric block diagonal
matrix with
is a symmetric block diagonal
matrix with 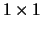 and
and 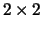 diagonal blocks.
The factored form of
diagonal blocks.
The factored form of  is then used to solve the above system.
is then used to solve the above system.
LA_HESV computes the solution to a linear system of
equations 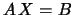 , where
, where  is a complex Hermitian
matrix and
is a complex Hermitian
matrix and 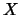 and
and 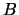 are rectangular matrices or vectors.
A diagonal pivoting method is used to factor
are rectangular matrices or vectors.
A diagonal pivoting method is used to factor  as
as
where 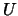 (or
(or 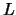 ) is a product of permutation
and unit upper (or lower) triangular matrices,
and
) is a product of permutation
and unit upper (or lower) triangular matrices,
and  is a complex Hermitian block
diagonal matrix with
is a complex Hermitian block
diagonal matrix with 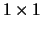 and
and 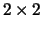 diagonal blocks.
The factored form of
diagonal blocks.
The factored form of  is then used to solve the above system.
is then used to solve the above system.





Next: Arguments
Up: Symmetric Indefinite Linear Systems
Previous: LA_SYSV / LA_HESV
Contents
Index
Susan Blackford
2001-08-19
![]() , where
, where ![]() is a real or complex symmetric
matrix and
is a real or complex symmetric
matrix and ![]() and
and ![]() are rectangular matrices or vectors.
A diagonal pivoting method is used to factor
are rectangular matrices or vectors.
A diagonal pivoting method is used to factor ![]() as
as