




Next: Examples
Up: Symmetric Indefinite Linear Systems
Previous: Purpose
Contents
Index
- A
- (input/output) REAL or COMPLEX square
array, shape
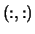 .
.
On entry, the matrix  .
.
If 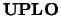 = 'U',
the upper triangular part of A contains the upper
triangular part
of the matrix
= 'U',
the upper triangular part of A contains the upper
triangular part
of the matrix  , and the strictly lower triangular part of
, and the strictly lower triangular part of
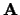 is not referenced.
is not referenced.
If 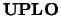 = 'L', the lower
triangular part of
= 'L', the lower
triangular part of 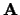 contains the lower triangular part of
the matrix
contains the lower triangular part of
the matrix  , and the strictly upper triangular part of
, and the strictly upper triangular part of 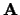 is not referenced.
is not referenced.
On exit, the block diagonal matrix  and the multipliers used to
obtain the factor
and the multipliers used to
obtain the factor 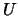 or
or 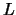 from the factorization of
from the factorization of  .
.
- B
- (input/output) REAL or COMPLEX array, shape
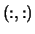 with
with
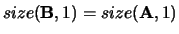 or shape
or shape 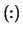 with
with
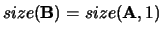 .
.
On entry, the matrix 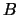 .
.
On exit, the solution matrix 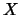 .
.
- UPLO
- Optional (input) CHARACTER(LEN=1)
![\begin{optionarg}
\item[{$=$\ 'U':}] Upper triangle of $A$\ is stored;
\item[{$=$\ 'L':}] Lower triangle of $A$\ is stored.
\end{optionarg}](img443.gif)
Default value: 'U'.
- IPIV
- Optional (output) INTEGER array, shape
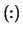 with
with
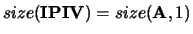 .
.
Details of the row and column interchanges and
the block structure of  .
.
If
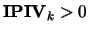 , then rows and columns
, then rows and columns 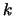 and
and
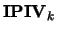 were interchanged, and
were interchanged, and 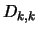 is a
is a
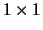 diagonal block.
diagonal block.
If
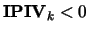 , then there are two cases:
, then there are two cases:

- INFO
- Optional (output) INTEGER
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if ${\bf IN...
...l matrix $D$\ is
singular, so the solution could not be computed.
\end{infoarg}](img475.gif)
If INFO is not present and an error occurs, then the program is
terminated with an error message.
References: [1] and [17,9,20,21].





Next: Examples
Up: Symmetric Indefinite Linear Systems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19
![\begin{optionarg}
\item[{$=$\ 'U':}] Upper triangle of $A$\ is stored;
\item[{$=$\ 'L':}] Lower triangle of $A$\ is stored.
\end{optionarg}](img443.gif)

![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if ${\bf IN...
...l matrix $D$\ is
singular, so the solution could not be computed.
\end{infoarg}](img475.gif)