




Next: Examples
Up: Generalized Symmetric Eigenvalue Problems
Previous: Purpose
Contents
Index
- AP
- (input/output) REAL or COMPLEX array,
shape
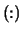 with
with
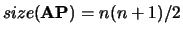 , where
, where 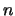 is the order of
is the order of  and
and 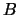 .
.
On entry, the upper or lower triangle of matrix
 in packed storage. The elements are stored columnwise as follows:
in packed storage. The elements are stored columnwise as follows:
On exit, the contents of AP are destroyed.
- BP
- (input/output) REAL or COMPLEX array,
shape
 and
and
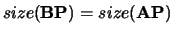 .
.
On entry, the upper or lower triangle of matrix
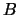 in packed storage. The elements are stored columnwise as follows:
in packed storage. The elements are stored columnwise as follows:
On exit, the triangular factor 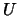 or
or 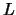 of the Cholesky
factorization
of the Cholesky
factorization 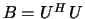 or
or 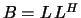 , in the same storage
format as
, in the same storage
format as 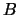 .
.
- W
- (output) REAL array, shape
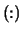 with
with
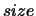 (W)
(W) 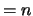 .
.
The eigenvalues in ascending order.
- ITYPE
- Optional (input) INTEGER.
Specifies the problem type to be solved:
![\begin{optionarg}
\item[{= 1:}] $A z = \lambda B z$ \item[{= 2:}] $A B z = \lambda z$ \item[{= 3:}] $B A z = \lambda z$ \end{optionarg}](img789.gif)
Default value: 1.
- UPLO
- Optional (input) CHARACTER(LEN=1).
![\begin{optionarg}
\item[{$ =$\ 'U':}] Upper triangles of $A$\ and $B$\ are stor...
...item[{$ =$\ 'L':}] Lower triangles of $A$\ and $B$\ are stored.
\end{optionarg}](img791.gif)
Default value: 'U'.
- Z
- Optional (output) REAL or COMPLEX
square array, shape
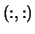 with
with 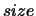 (Z,1)
(Z,1) 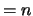 .
.
The matrix 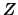 of eigenvectors, normalized as follows:
of eigenvectors, normalized as follows:
![\begin{optionarg}
\item[{if ${\bf ITYPE} = 1$\ or $2$:}] $Z^H\,B\,Z = I$,
\item[{if ${\bf ITYPE} = 3$:}] $Z^H\,B^{-1}\,Z = I$.
\end{optionarg}](img786.gif)
- INFO
- Optional (output) INTEGER.
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INF...
...d and
no eigenvalues or eigenvectors were computed.
\end{infoarg}\end{infoarg}](img814.gif)
If INFO is not present and an error occurs, then the
program is terminated with an error message.
References: [1] and [17,9,20].





Next: Examples
Up: Generalized Symmetric Eigenvalue Problems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19
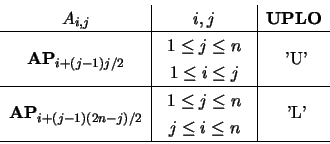
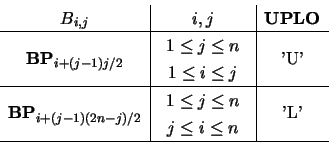
![\begin{optionarg}
\item[{= 1:}] $A z = \lambda B z$ \item[{= 2:}] $A B z = \lambda z$ \item[{= 3:}] $B A z = \lambda z$ \end{optionarg}](img789.gif)
![\begin{optionarg}
\item[{$ =$\ 'U':}] Upper triangles of $A$\ and $B$\ are stor...
...item[{$ =$\ 'L':}] Lower triangles of $A$\ and $B$\ are stored.
\end{optionarg}](img791.gif)
![\begin{optionarg}
\item[{if ${\bf ITYPE} = 1$\ or $2$:}] $Z^H\,B\,Z = I$,
\item[{if ${\bf ITYPE} = 3$:}] $Z^H\,B^{-1}\,Z = I$.
\end{optionarg}](img786.gif)
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INF...
...d and
no eigenvalues or eigenvectors were computed.
\end{infoarg}\end{infoarg}](img814.gif)