




Next: Arguments
Up: Standard Singular Value Problems
Previous: LA_GESVD / LA_GESDD
Contents
Index
LA_GESVD and LA_GESDD compute the singular values and,
optionally, the left and/or right singular vectors from the
singular value decomposition (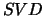 ) of a real or complex
) of a real or complex 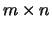 matrix
matrix  .
The
.
The 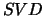 of
of  is written
is written
where 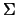 is an
is an 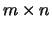 matrix which is zero except for its
matrix which is zero except for its
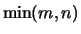 diagonal elements,
diagonal elements, 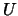 is an
is an 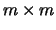 orthogonal (unitary)
matrix, and
orthogonal (unitary)
matrix, and 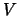 is an
is an 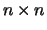 orthogonal (unitary) matrix. The
diagonal elements of
orthogonal (unitary) matrix. The
diagonal elements of 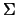 , i.e., the values
, i.e., the values
are the singular values of  ; they are real and non-negative, and
are returned in descending order. The first
; they are real and non-negative, and
are returned in descending order. The first 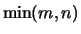 columns of
columns of
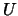 and
and 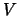 are the left and right singular vectors of
are the left and right singular vectors of  , respectively.
, respectively.
LA_GESDD solves the same problem as LA_GESVD but uses a divide and
conquer method if singular vectors are desired. For large matrices it is usually much
faster than LA_GESVD when singular vectors are desired, but uses more workspace.
Note: The routine returns 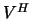 , not
, not 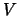 .
.





Next: Arguments
Up: Standard Singular Value Problems
Previous: LA_GESVD / LA_GESDD
Contents
Index
Susan Blackford
2001-08-19
![]() ) of a real or complex
) of a real or complex ![]() matrix
matrix ![]() .
The
.
The ![]() of
of ![]() is written
is written
![]() , not
, not ![]() .
.