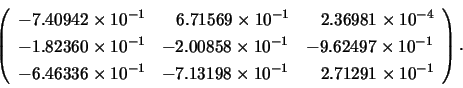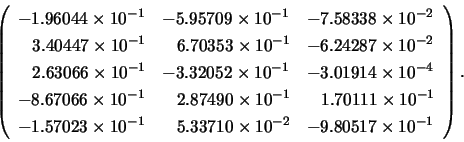Next: Generalized Singular Value Problems
Up: Examples
Previous: Example 1 (from Program
Contents
Index
Matrix  as in Example 1.
as in Example 1.
The call:
CALL LA_GESVD( A, S, VT=VT, WW=WW, JOB='U', INFO=INFO )
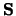 on exit: as in Example 1.
on exit: as in Example 1.
A, VT, WW, and INFO on exit:
The singular values of  are the same as in Example 1.
are the same as in Example 1.
The left singular vectors of  are:
are:
The right singular vectors of  are (columnwise):
are (columnwise):
Susan Blackford
2001-08-19
![]() on exit: as in Example 1.
on exit: as in Example 1.


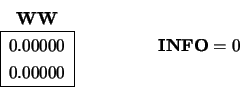
![]() are:
are: