




Next: Arguments
Up: Generalized Singular Value Problems
Previous: LA_GGSVD
Contents
Index
LA_GGSVD computes the generalized singular values and,
optionally, the transformation matrices from the generalized
singular value decomposition
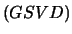 of a real or complex matrix pair
of a real or complex matrix pair 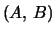 , where
, where  is
is 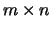 and
and 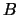 is
is 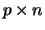 . The
. The 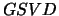 of
of 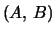 is written
is written
where 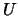 ,
, 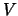 and
and 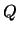 are orthogonal (unitary) matrices of
dimensions
are orthogonal (unitary) matrices of
dimensions 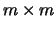 ,
, 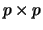 and
and 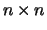 , respectively.
Let
, respectively.
Let 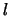 be the rank of
be the rank of 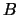 and
and 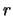 the rank of the
the rank of the 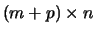 matrix
matrix
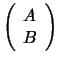 , and let
, and let 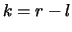 .
Then
.
Then 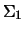 and
and 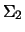 are
are
 and
and
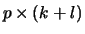 ``diagonal'' matrices, respectively, and
``diagonal'' matrices, respectively, and 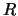 is a
is a
 nonsingular upper triangular matrix. The detailed structure of
nonsingular upper triangular matrix. The detailed structure of 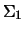 ,
,
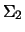 and R depends on the sign of
and R depends on the sign of 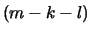 as follows:
as follows:
The case
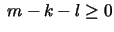 :
:
where 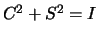 . We define
. We define
The case  :
:
where 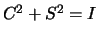 . We define
. We define
In both cases the generalized singular values of the pair 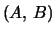 are the ratios
are the ratios
The first 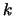 singular values are infinite. The finite singular
values are real and nonnegative.
singular values are infinite. The finite singular
values are real and nonnegative.
LA_GGSVD computes the real (nonnegative) scalars
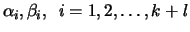 , the matrix
, the matrix 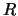 ,
and, optionally, the transformation matrices
,
and, optionally, the transformation matrices 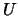 ,
, 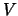 and
and 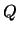 .
.
Note: Some important special cases of the 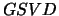 are given in
Section 2.2.5.3.
are given in
Section 2.2.5.3.





Next: Arguments
Up: Generalized Singular Value Problems
Previous: LA_GGSVD
Contents
Index
Susan Blackford
2001-08-19
![]() of a real or complex matrix pair
of a real or complex matrix pair ![]() , where
, where ![]() is
is ![]() and
and ![]() is
is ![]() . The
. The ![]() of
of ![]() is written
is written
 , and let
, and let 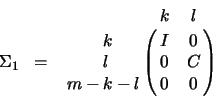
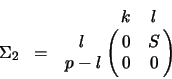
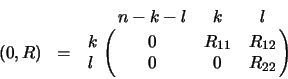

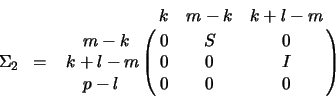

![]() are given in
Section 2.2.5.3.
are given in
Section 2.2.5.3.