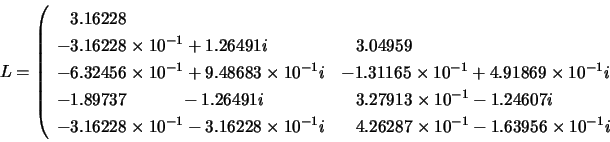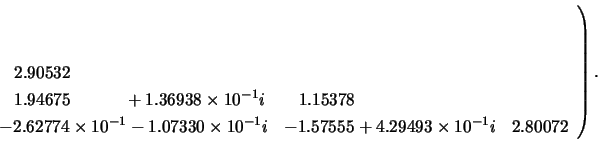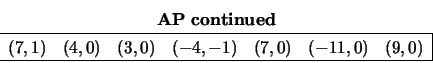


The call:
CALL LA_HPGV( AP, BP, W, 3, 'L', Z, INFO )
![]() ,
, ![]() ,
, ![]() , and
, and ![]() on exit:
on exit:

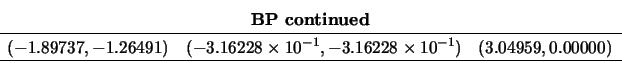
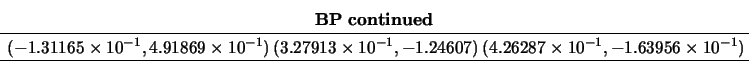





The eigenvalues of the problem
![]() are:
are:

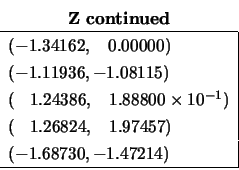
The eigenvectors are:
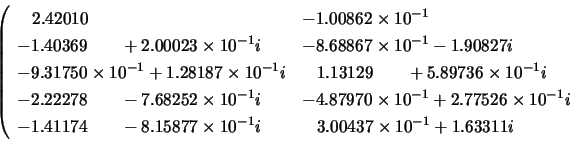

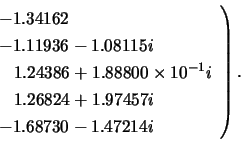
The triangular factor ![]() from the Cholesky factorization of
from the Cholesky factorization of ![]() is:
is: