




Next: Arguments
Up: Standard Nonsymmetric Eigenvalue Problems
Previous: LA_GEEVX
Contents
Index
LA_GEEVX computes for a real or complex square matrix  , the
eigenvalues and, optionally, the left and/or right eigenvectors.
Optionally, it also balances
, the
eigenvalues and, optionally, the left and/or right eigenvectors.
Optionally, it also balances  and computes
reciprocal condition numbers for the eigenvalues and right
eigenvectors.
and computes
reciprocal condition numbers for the eigenvalues and right
eigenvectors.
A right eigenvector 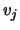 of
of  satisfies
satisfies
where 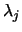 is its eigenvalue.
A left eigenvector
is its eigenvalue.
A left eigenvector 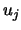 of
of  satisfies
satisfies
where 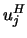 denotes the conjugate transpose of
denotes the conjugate transpose of 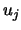 .
The computed eigenvectors are normalized to have Euclidean norm
equal to
.
The computed eigenvectors are normalized to have Euclidean norm
equal to 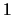 and largest component real.
and largest component real.
Balancing  involves permuting its rows and columns to
make it more nearly upper triangular and then scaling rows and
columns by a diagonal similarity transformation to reduce the
condition numbers of the eigenvalues and eigenvectors.
involves permuting its rows and columns to
make it more nearly upper triangular and then scaling rows and
columns by a diagonal similarity transformation to reduce the
condition numbers of the eigenvalues and eigenvectors.
Computed reciprocal condition numbers pertain to the matrix
after balancing. Permuting does not change
condition numbers (in exact arithmetic), but scaling does.





Next: Arguments
Up: Standard Nonsymmetric Eigenvalue Problems
Previous: LA_GEEVX
Contents
Index
Susan Blackford
2001-08-19
![]() , the
eigenvalues and, optionally, the left and/or right eigenvectors.
Optionally, it also balances
, the
eigenvalues and, optionally, the left and/or right eigenvectors.
Optionally, it also balances ![]() and computes
reciprocal condition numbers for the eigenvalues and right
eigenvectors.
and computes
reciprocal condition numbers for the eigenvalues and right
eigenvectors.
![]() of
of ![]() satisfies
satisfies