Arguments

AB

(input/output) REAL or COMPLEX array, shape $(:,:)$ with $size$(AB,1) $= ka+1$ and $size$(AB,2) $= n$, where $ka$ is the number of subdiagonals or superdiagonals in the band and $n$ is the order of $A$ and $B$.
On entry, the upper (if UPLO = 'U') or lower (if UPLO = 'L') triangle of matrix $A$ in band storage. The $ka+1$ diagonals of $A$ are stored in the rows of AB so that the $j^{th}$ column of $A$ is stored in the $j^{th}$ column of ${\bf AB}$ as follows:

$$\begin{array}{c\vert c\vert c} A_{i,j} & i,j & {\bf UPLO} ... ...1 \leq j \leq n \end{array} & \mbox{'L'} \\ \hline \end{array}$$

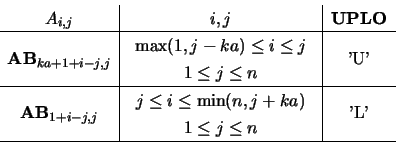
On exit, the contents of AB are destroyed.

BB

(input/output) REAL or COMPLEX array, shape $(:,:)$ with $size$(BB,1) $= kb+1$ and $size$(BB,2) $= n$, where $kb$ is the number of subdiagonals or superdiagonals in the band of $B$.
On entry, the upper (if UPLO = 'U') or lower (if UPLO = 'L') triangle of matrix $B$ in band storage. The $kb+1$ diagonals of $B$ are stored in the rows of BB so that the $j^{th}$ column of $B$ is stored in the $j^{th}$ column of ${\bf BB}$ as follows:

$$\begin{array}{c\vert c\vert c} B_{i,j} & i,j & {\bf UPLO} ... ...1 \leq j \leq n \end{array} & \mbox{'L'} \\ \hline \end{array}$$

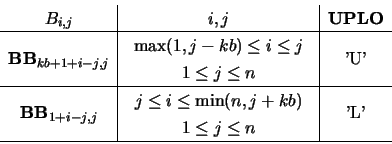
On exit, the factor $S$ from the split Cholesky factorization $B = S^H\,S$.

W

(output) REAL array, shape $(:)$ with $size$(W) $= n$.
The eigenvalues in ascending order.

UPLO

Optional (input) CHARACTER(LEN=1).


Default value: 'U'.

Z

Optional (output) REAL or COMPLEX square array, shape $(:,:)$ with $size$(Z,1) $= n$ .
The matrix $Z$ of eigenvectors, normalized so that $Z^H\,B\,Z = I$.

INFO

Optional (output) INTEGER.


If INFO is not present and an error occurs, then the program is terminated with an error message.

References: [1] and [17,9,20].