- ...Vincent A. Barker1
- Department of Mathematical Modelling (IMM),
Technical University of Denmark, Building 305, DK-2800
Lyngby, Denmark; email: vab@imm.dtu.dk
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Blackford2
- Department of Computer Science,
University of Tennessee, 1122 Volunteer Blvd., Suite 203, Knoxville,
TN 37996-3450, USA; email susan@cs.utk.edu
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Jack J. Dongarra3
- Department of Computer Science,
University of Tennessee, 1122 Volunteer Blvd., Suite 203, Knoxville,
TN 37996-3450, USA; email: dongarra@cs.utk.edu
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Jeremy Du Croz4
- Numerical Algorithms Group Ltd,
Wilkinson House, Jordan Hill Road, Oxford OX2 8DR, UK;
email: jeremy@nag.co.uk
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Sven Hammarling5
- Numerical Algorithms Group Ltd,
Wilkinson House, Jordan Hill Road, Oxford OX2 8DR, UK;
email: sven@nag.co.uk
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Minka Marinova6
- The Danish Computing Center for
Research and Education (UNI
 C),
Technical University of Denmark, Lyngby,
Denmark; Email: Minka.Marinova@uni-c.dk
C),
Technical University of Denmark, Lyngby,
Denmark; Email: Minka.Marinova@uni-c.dk
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...sniewski7
- The Danish Computing Center for
Research and Education (UNI
 C),
Technical University of Denmark, Bldg. 304, DK-2800 Lyngby,
Denmark; Email: jerzy.wasniewski@uni-c.dk
C),
Technical University of Denmark, Bldg. 304, DK-2800 Lyngby,
Denmark; Email: jerzy.wasniewski@uni-c.dk
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Yalamov8
- Center of Applied Mathematics and Informatics,
University of Rousse, Bulgaria; Email: yalamov@ami.ru.acad.bg
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... defined2.1
- If we tried
to compute the trivial eigenvalues in the same way as the nontrivial
ones, that is by taking ratios of the leading
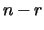 diagonal entries
of
diagonal entries
of 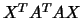 and
and 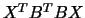 , we would get 0/0. For a detailed
mathematical discussion of this decomposition, see the discussion of
the Kronecker Canonical Form in [19].
, we would get 0/0. For a detailed
mathematical discussion of this decomposition, see the discussion of
the Kronecker Canonical Form in [19].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... output)3.1
-
(Input or output) means that the argument may be either an input argument or
an output argument, depending on the values of other arguments.
For example, in the xyySVX driver routines, some arguments are used either
as output arguments to return details of a factorization, or as input
arguments to supply details of a previously computed factorization.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... )6.1
- wp ::= KIND( 1.0)
 KIND( 1.0D0)
KIND( 1.0D0)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 6.2
wp ::= KIND( 1.0)  KIND( 1.0D0)
KIND( 1.0D0)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... )7.1
wp is a work precision; wp ::= KIND( 1.0)  KIND( 1.0D0)
KIND( 1.0D0)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... )7.2
wp ::= KIND( 1.0)  KIND( 1.0D0)
KIND( 1.0D0)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... )7.3
wp ::= KIND( 1.0)  KIND( 1.0D0)
KIND( 1.0D0)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... )7.4
wp ::= KIND( 1.0)  KIND( 1.0D0)
KIND( 1.0D0)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... )7.5
wp is a work precision; wp ::= KIND( 1.0)  KIND( 1.0D0)
KIND( 1.0D0)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... )8.1
wp ::= KIND( 1.0)  KIND( 1.0D0)
KIND( 1.0D0)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... )8.2
wp ::= KIND( 1.0)  KIND( 1.0D0)
KIND( 1.0D0)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.