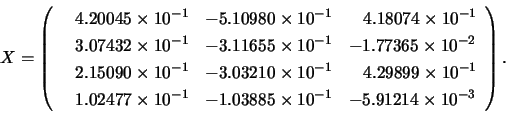Example (from Program LA_GELSS_EXAMPLE)

The results below are computed with $\epsilon = 1.19209 \times 10^{-7}$.
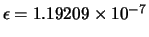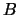Matrices $A$ and $B$ are the same as in the example for LA_GELSY. The call:
CALL LA_GELSS( A, B, RANK, S, RCOND=0.00001_wp, INFO=INFO ) ^6.2

A, B, S, RANK, and INFO on exit:

$$\begin{array}{c} {\bf A} \\ \begin{array}{\vert llll\vert... ...\;\; 6.90588 \times 10^{-1} \\ \hline \end{array} \end{array}$$

$$\hspace{-1.00 cm} \begin{array}{c} {\bf B} \\ \begin{array... ...\\ 7.52832 \times 10^{-15} \\ \hline \end{array} \end{array}$$

$$\begin{array}{c} {\bf RANK} = 2 \end{array}\hspace{1.00 cm} \begin{array}{c} {\bf INFO} = 0 \end{array}$$

The singular values of $A$ are:

$$\left( \begin{array}{llll} 13.7210 & 6.14279 & 2.64806 \times 10^{-7} & 7.52832 \times 10^{-15} \end{array} \right)$$

The right singular vectors are (columnwise):

$$\left( \begin{array}{llll} -1.14937 \times 10^{-1} & -7.55... ...0 \times 10^{-1} & -8.16497 \times 10^{-1} \end{array} \right)$$

The solution matrix is:

$$X = \left( \begin{array}{lll} \;\;\; 4.20045 \times 10^{-1} ... ...mes 10^{-1} & -5.91214 \times 10^{-3} \\ \end{array} \right).$$