




Next: Implicit Restart
Up: Implicitly Restarted Arnoldi Method
Previous: Implicitly Restarted Arnoldi Method
Contents
Index
To begin our discussion, we shall look at the Arnoldi procedure
from a slightly different perspective.
The Arnoldi procedure was derived previously in
§7.5 and
has been presented in modified Gram-Schmidt algorithmic form in
Algorithm 7.3.
In this section, we describe it in matrix-vector (or GEMV) form using
the classical Gram-Schmidt process together with the orthogonalization
refinement [96]. The Arnoldi relation between
the matrix  , the basis matrix
, the basis matrix 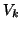 , and the residual vector
, and the residual vector 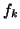 is of the form
is of the form
where
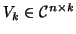 has orthonormal columns,
has orthonormal columns,
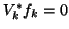 ,
and
,
and
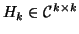 is upper
Hessenberg with nonnegative subdiagonal elements. We shall call this
a k-step Arnoldi factorization of
is upper
Hessenberg with nonnegative subdiagonal elements. We shall call this
a k-step Arnoldi factorization of  .
It is easily seen from the construction
that
.
It is easily seen from the construction
that
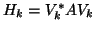 is upper Hessenberg.
When
is upper Hessenberg.
When  is Hermitian, this implies that
is Hermitian, this implies that
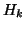 is real symmetric and tridiagonal. The columns
of
is real symmetric and tridiagonal. The columns
of 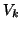 are referred to as the Arnoldi vectors.
are referred to as the Arnoldi vectors.
A template for computing a 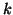 -step Arnoldi
factorization is given in Algorithm 7.6.
-step Arnoldi
factorization is given in Algorithm 7.6.
![\begin{algorithm}{$k$-Step Arnoldi Factorization
}
{
\begin{tabbing}
(nr)ss\=i...
...t{H}_{j}, h]$\ \\
{\rm (18)} \> \>{\bf end for}
\end{tabbing}}
\end{algorithm}](img1966.png)
We will now describe some implementation details, referring to the
respective phases in Algorithm 7.6.
- (1)
- Choose the initial starting vector
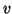 and normalize. Ideally, for eigenvalue
calculations, one should attempt to construct a
and normalize. Ideally, for eigenvalue
calculations, one should attempt to construct a 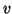 that is dominant
in eigenvector directions of interest. In the absence of any other
considerations, a random vector is a reasonable choice.
that is dominant
in eigenvector directions of interest. In the absence of any other
considerations, a random vector is a reasonable choice.
- (2)
- Initialize the Arnoldi procedure. In the subsequent step,
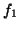 will
become the new Arnoldi basis vector. This step should include
a reorthogonalization just as all of the others do.
will
become the new Arnoldi basis vector. This step should include
a reorthogonalization just as all of the others do.
- (7)
- Normalize
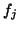 to get the new basis vector
to get the new basis vector 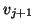 , partially
update
, partially
update 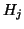 to get the
to get the
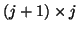 matrix
matrix 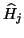 ,
and compute the new information
,
and compute the new information
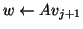 .
The norm calculation
.
The norm calculation
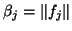 need not be recomputed
here. It has already been computed at step (12) and can be saved for reuse
here.
need not be recomputed
here. It has already been computed at step (12) and can be saved for reuse
here.
- (10)
- This is the classical Gram-Schmidt step to orthogonalize
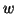 with
respect to the columns of
with
respect to the columns of 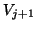 .
This formulation allows
level 2 matrix-vector operations. A more detailed discussion
is given below.
.
This formulation allows
level 2 matrix-vector operations. A more detailed discussion
is given below.
- (12)
- The sequence of statements in this if-clause assure that the
new direction
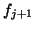 is numerically orthogonal to the previously
computed directions, i.e., to the columns of
is numerically orthogonal to the previously
computed directions, i.e., to the columns of 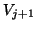 . The parameter
. The parameter 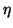 must be specified (
must be specified (
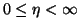 ).
The test asks the question, ``Is
).
The test asks the question, ``Is 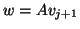 nearly in
the space that already has been constructed?"
The ratio
nearly in
the space that already has been constructed?"
The ratio
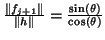 ,
where
,
where 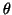 is the angle that the vector
is the angle that the vector 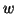 makes with
makes with
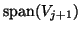 (i.e., the angle
(i.e., the angle 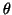 between
between 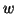 and its projection
and its projection 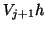 ).
A larger value of
).
A larger value of 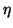 is a more stringent orthogonality requirement.
With
is a more stringent orthogonality requirement.
With 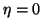 the algorithm reverts to classical Gram-Schmidt (CGS).
An additional detail is needed to completely specify this process.
If, after updating
the algorithm reverts to classical Gram-Schmidt (CGS).
An additional detail is needed to completely specify this process.
If, after updating 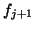 and
and 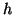 , the
relation
, the
relation
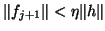 still holds,
then numerically we have
still holds,
then numerically we have
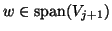 . In this case,
the Arnoldi procedure should either be terminated or a randomly generated
vector should be orthogonalized with respect to the columns of
. In this case,
the Arnoldi procedure should either be terminated or a randomly generated
vector should be orthogonalized with respect to the columns of 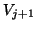 to replace
to replace 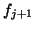 , and
, and 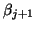 should be set to zero
to continue the factorization. The value of
should be set to zero
to continue the factorization. The value of 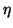 used in
the ARPACK implementation is
used in
the ARPACK implementation is 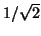 (see §7.6.9).
Additional discussion of this orthogonalization device is given below.
(see §7.6.9).
Additional discussion of this orthogonalization device is given below.
- (17)
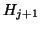 is now a
is now a
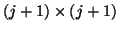 upper Hessenberg matrix.
upper Hessenberg matrix.
The dense matrix-vector products
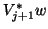 and
and 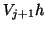 may be expressed with the Level 2 BLAS operation GEMV.
This provides a significant performance advantage on virtually
every platform from workstation to supercomputer. Moreover, considerable
effort has been made within the ScaLAPACK
project [52] and also by several high-performance computer
vendors to optimize these kernels for a variety of parallel machines.
may be expressed with the Level 2 BLAS operation GEMV.
This provides a significant performance advantage on virtually
every platform from workstation to supercomputer. Moreover, considerable
effort has been made within the ScaLAPACK
project [52] and also by several high-performance computer
vendors to optimize these kernels for a variety of parallel machines.
The mechanism used to orthogonalize the new information 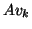 against the existing basis
against the existing basis 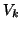 is the CGS.
It is notoriously unstable and will fail miserably in this setting
without modification. One remedy is to use the modified Gram-Schmidt
process as used in Algorithm 7.3.
Unfortunately, this will also fail
to produce orthogonal vectors in the restarting situation we are
about to discuss and it cannot be expressed with Level 2 BLAS in this setting.
At step (5), we have included an iterative refinement technique
proposed by Daniel, Gragg, Kaufman, and Stewart (DGKS)
in [96]. This scheme provides an excellent way to construct
a vector
is the CGS.
It is notoriously unstable and will fail miserably in this setting
without modification. One remedy is to use the modified Gram-Schmidt
process as used in Algorithm 7.3.
Unfortunately, this will also fail
to produce orthogonal vectors in the restarting situation we are
about to discuss and it cannot be expressed with Level 2 BLAS in this setting.
At step (5), we have included an iterative refinement technique
proposed by Daniel, Gragg, Kaufman, and Stewart (DGKS)
in [96]. This scheme provides an excellent way to construct
a vector 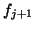 that is numerically orthogonal to
that is numerically orthogonal to 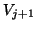 .
The simple test specified at step (5) is used to avoid
this DGKS correction if it is not needed.
.
The simple test specified at step (5) is used to avoid
this DGKS correction if it is not needed.
This mechanism maintains orthogonality to full working precision at
very reasonable cost. The special situation imposed by the restarting
scheme we are about to discuss makes this modification essential for
obtaining accurate eigenvalues and numerically orthogonal Schur
vectors (eigenvectors in the Hermitian case). Schemes based on MGS
are often sufficient for solving linear systems because they do
construct a basis set that is linearly independent even though
it might not be numerically orthogonal. The quality of MGS orthogonality
is dependent upon the condition number (linear independence)
of the original set of vectors. The implicit restarting mechanism we
are about to present will be less effective and may even fail if numerical
orthogonality is not maintained.
It has been well documented that failure to maintain orthogonality
leads to several numerical difficulties within the Lanczos or
Arnoldi procedure.
In the Hermitian case, Paige [347] showed
that the loss of orthogonality occurs precisely
when an eigenvalue of 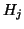 is close to an eigenvalue of
is close to an eigenvalue of 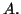 In fact, the
Arnoldi vectors lose orthogonality in the direction of the associated
approximate eigenvector. Moreover, failure to maintain
orthogonality results in spurious copies of the approximate eigenvalue
produced by the Arnoldi method. In the Hermitian case, several
remedies short of full reorthogonalization have been proposed.
These are discussed in §4.4 (p.
In fact, the
Arnoldi vectors lose orthogonality in the direction of the associated
approximate eigenvector. Moreover, failure to maintain
orthogonality results in spurious copies of the approximate eigenvalue
produced by the Arnoldi method. In the Hermitian case, several
remedies short of full reorthogonalization have been proposed.
These are discussed in §4.4 (p. ![[*]](http://www.netlib.org/utk/icons/crossref.png) ).
).





Next: Implicit Restart
Up: Implicitly Restarted Arnoldi Method
Previous: Implicitly Restarted Arnoldi Method
Contents
Index
Susan Blackford
2000-11-20
![]() -step Arnoldi
factorization is given in Algorithm 7.6.
-step Arnoldi
factorization is given in Algorithm 7.6.
![]() against the existing basis
against the existing basis ![]() is the CGS.
It is notoriously unstable and will fail miserably in this setting
without modification. One remedy is to use the modified Gram-Schmidt
process as used in Algorithm 7.3.
Unfortunately, this will also fail
to produce orthogonal vectors in the restarting situation we are
about to discuss and it cannot be expressed with Level 2 BLAS in this setting.
At step (5), we have included an iterative refinement technique
proposed by Daniel, Gragg, Kaufman, and Stewart (DGKS)
in [96]. This scheme provides an excellent way to construct
a vector
is the CGS.
It is notoriously unstable and will fail miserably in this setting
without modification. One remedy is to use the modified Gram-Schmidt
process as used in Algorithm 7.3.
Unfortunately, this will also fail
to produce orthogonal vectors in the restarting situation we are
about to discuss and it cannot be expressed with Level 2 BLAS in this setting.
At step (5), we have included an iterative refinement technique
proposed by Daniel, Gragg, Kaufman, and Stewart (DGKS)
in [96]. This scheme provides an excellent way to construct
a vector ![]() that is numerically orthogonal to
that is numerically orthogonal to ![]() .
The simple test specified at step (5) is used to avoid
this DGKS correction if it is not needed.
.
The simple test specified at step (5) is used to avoid
this DGKS correction if it is not needed.
![]() is close to an eigenvalue of
is close to an eigenvalue of ![]() In fact, the
Arnoldi vectors lose orthogonality in the direction of the associated
approximate eigenvector. Moreover, failure to maintain
orthogonality results in spurious copies of the approximate eigenvalue
produced by the Arnoldi method. In the Hermitian case, several
remedies short of full reorthogonalization have been proposed.
These are discussed in §4.4 (p.
In fact, the
Arnoldi vectors lose orthogonality in the direction of the associated
approximate eigenvector. Moreover, failure to maintain
orthogonality results in spurious copies of the approximate eigenvalue
produced by the Arnoldi method. In the Hermitian case, several
remedies short of full reorthogonalization have been proposed.
These are discussed in §4.4 (p. ![]() ).
).