




Next: Error Bounds for Computed
Up: Positive Definite
Previous: Transfer Residual Error to
Contents
Index
Error Bounds for Computed Eigenvalues.
Rewrite 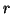 as
as
By (4.54) on p. ![[*]](http://www.netlib.org/utk/icons/crossref.png) , we have
, we have
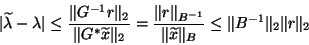 |
(95) |
for some eigenvalue  of the pair
of the pair 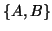 .
A good estimate to
.
A good estimate to  is needed to use this bound.
is needed to use this bound.
With more information, a much better bound
can be obtained.
Let us assume that
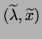 is
an approximation of the eigenpair
is
an approximation of the eigenpair 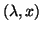 of the pair.
The ``best''
of the pair.
The ``best'' 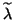 corresponding to
corresponding to 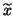 is the Rayleigh quotient
is the Rayleigh quotient
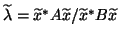 ,
so we assume that
,
so we assume that 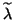 has this value.
Suppose that
has this value.
Suppose that 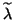 is closer
to
is closer
to  than any other eigenvalues of the pair, and
let
than any other eigenvalues of the pair, and
let 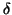 be the gap between
be the gap between
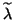 and any other eigenvalue of the pair. Then
and any other eigenvalue of the pair. Then
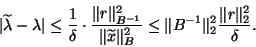 |
(96) |
This improves (5.31) if the gap 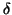 is
reasonably big. In practice we can always pick the better one.
This bound also needs information on
is
reasonably big. In practice we can always pick the better one.
This bound also needs information on
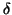 , besides the residual error
, besides the residual error 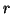 and
and 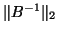 .
Usually such information
is available after a successful computation by,
e.g., the shift-and-invert Lanczos
algorithm, which usually delivers eigenvalues in the neighborhood
of a shift and consequently yields good information on the
.
Usually such information
is available after a successful computation by,
e.g., the shift-and-invert Lanczos
algorithm, which usually delivers eigenvalues in the neighborhood
of a shift and consequently yields good information on the
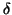 . This comment also applies to the bounds in
(5.33) and (5.34)
below.
. This comment also applies to the bounds in
(5.33) and (5.34)
below.





Next: Error Bounds for Computed
Up: Positive Definite
Previous: Transfer Residual Error to
Contents
Index
Susan Blackford
2000-11-20
![]() is
an approximation of the eigenpair
is
an approximation of the eigenpair ![]() of the pair.
The ``best''
of the pair.
The ``best'' ![]() corresponding to
corresponding to ![]() is the Rayleigh quotient
is the Rayleigh quotient
![]() ,
so we assume that
,
so we assume that ![]() has this value.
Suppose that
has this value.
Suppose that ![]() is closer
to
is closer
to ![]() than any other eigenvalues of the pair, and
let
than any other eigenvalues of the pair, and
let ![]() be the gap between
be the gap between
![]() and any other eigenvalue of the pair. Then
and any other eigenvalue of the pair. Then