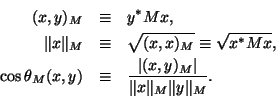Next: Residual Vector.
Up: Stability and Accuracy Assessments
Previous: Stability and Accuracy Assessments
Contents
Index
We reduce it to an equivalent standard HEP.
It is done as follows. Choose a decomposition for  :
:
 |
(90) |
Then the generalized eigenvalue problem for 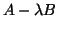 is equivalent to the standard HEP
for
is equivalent to the standard HEP
for 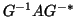 . Both share the same eigenvalues since
. Both share the same eigenvalues since
which also says that if 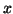 is an eigenvector for the pair,
is an eigenvector for the pair,
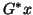 is an eigenvector for the matrix
is an eigenvector for the matrix 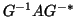 , and on the
other hand if
, and on the
other hand if 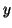 is an eigenvector for
is an eigenvector for 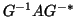 ,
,
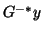 is an eigenvector for the pair.
Common choices for
is an eigenvector for the pair.
Common choices for 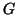 are:
are:
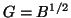 , the unique positive definite square root of
, the unique positive definite square root of  .
In this case,
.
In this case, 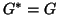 . This choice is good enough for
theoretical investigations.
. This choice is good enough for
theoretical investigations.
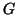 is the Cholesky factor; optionally with pivoting,
i.e.,
is the Cholesky factor; optionally with pivoting,
i.e., 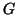 is lower triangular with positive diagonal entries. This choice is preferred for
numerical computations.
is lower triangular with positive diagonal entries. This choice is preferred for
numerical computations.
- Analogously
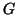 is upper triangular with positive diagonal
entries. It shares the same advantage of the second choice.
is upper triangular with positive diagonal
entries. It shares the same advantage of the second choice.
In what follows, sometimes it is more convenient to use the inner
product
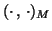 induced by a positive definite matrix
induced by a positive definite matrix 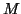 ,
the corresponding vector norm
,
the corresponding vector norm 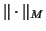 , and the two-vector angle function
(more precisely, angle between the subspaces spanned by two vectors)
, and the two-vector angle function
(more precisely, angle between the subspaces spanned by two vectors)
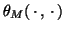 .
In our case,
.
In our case, 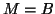 or
or 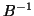 . They are defined as follows.
. They are defined as follows.
When 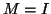 , all three reduce to the usual
definitions. It is rather easy to see that
, all three reduce to the usual
definitions. It is rather easy to see that
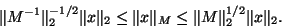 |
(91) |
With some extra work,
we can relate 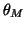 to the usual angle function, e.g., for
to the usual angle function, e.g., for 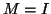 ,
as follows.
,
as follows.
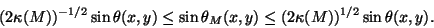 |
(92) |
Subsections





Next: Residual Vector.
Up: Stability and Accuracy Assessments
Previous: Stability and Accuracy Assessments
Contents
Index
Susan Blackford
2000-11-20