




Next: Remarks on Clustered Eigenvalues.
Up: Positive Definite
Previous: Error Bounds for Computed
Contents
Index
Error Bounds for Computed Eigenvectors.
Keep the assignments to 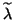 ,
, 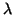 , and
, and 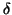 as above, and
let
as above, and
let 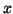 be the eigenvector of
be the eigenvector of 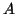 corresponding to
corresponding to 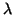 .
The error bound for the computed eigenvector
.
The error bound for the computed eigenvector 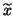 and the
true eigenvector
and the
true eigenvector 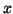 are
are
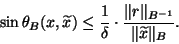 |
(97) |
This, (5.27), and (5.28)
yield
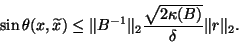 |
(98) |
The factor 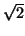 can be removed
by a more elaborate argument, but we shall omit it here.
can be removed
by a more elaborate argument, but we shall omit it here.
Susan Blackford
2000-11-20