




Next: Error Bounds for Computed
Up: Positive Definite
Previous: Residual Vector.
Contents
Index
Transfer Residual Error to Backward Error.
It can be proved that there are Hermitian matrices 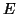 , e.g.,
, e.g.,
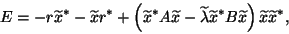 |
(93) |
such that 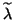 and
and 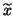 are an exact eigenvalue and
its corresponding eigenvector of
are an exact eigenvalue and
its corresponding eigenvector of 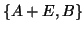 .
We are interested in such matrices
.
We are interested in such matrices 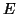 with smallest possible norms.
It turns out the best possible
with smallest possible norms.
It turns out the best possible 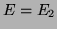 for the spectral norm
for the spectral norm 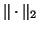 and the best possible
and the best possible 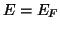 for the Frobenius norm
for the Frobenius norm 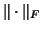 satisfy
satisfy
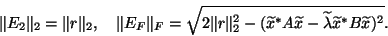 |
(94) |
See [256,431,473].
In fact, 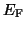 is given explicitly by (5.29).
So if
is given explicitly by (5.29).
So if 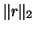 is small, the computed
is small, the computed 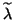 and
and 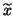 are exact ones of nearby matrices.
Error analysis of
this kind is called backward error analysis and
matrices
are exact ones of nearby matrices.
Error analysis of
this kind is called backward error analysis and
matrices 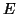 are backward errors.
are backward errors.
We say an algorithm
that delivers an approximate eigenpair
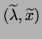 is
is
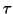 -backward stable for the pair with
respect to the norm
-backward stable for the pair with
respect to the norm 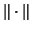 if it is an exact eigenpair for
if it is an exact eigenpair for 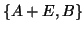 with
with 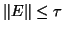 .
With these in mind,
statements can be made about the backward stability of the algorithm which
computes the eigenpair
.
With these in mind,
statements can be made about the backward stability of the algorithm which
computes the eigenpair
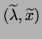 .
In convention, an algorithm is called backward stable
if
.
In convention, an algorithm is called backward stable
if
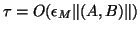 , where
, where
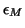 is the machine precision.
is the machine precision.





Next: Error Bounds for Computed
Up: Positive Definite
Previous: Residual Vector.
Contents
Index
Susan Blackford
2000-11-20
![]() is
is
![]() -backward stable for the pair with
respect to the norm
-backward stable for the pair with
respect to the norm ![]() if it is an exact eigenpair for
if it is an exact eigenpair for ![]() with
with ![]() .
With these in mind,
statements can be made about the backward stability of the algorithm which
computes the eigenpair
.
With these in mind,
statements can be made about the backward stability of the algorithm which
computes the eigenpair
![]() .
In convention, an algorithm is called backward stable
if
.
In convention, an algorithm is called backward stable
if
![]() , where
, where
![]() is the machine precision.
is the machine precision.