




Next: Implicit Restart
Up: Hermitian Eigenvalue Problems
Previous: Results for L-Shaped Membrane
Contents
Index
Implicitly Restarted Lanczos Method
R. Lehoucq and D. Sorensen
The Lanczos process for a Hermitian matrix 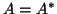 has been
derived previously in §4.4.
Here, we discuss how to apply
implicit restart.
Our starting point is a
has been
derived previously in §4.4.
Here, we discuss how to apply
implicit restart.
Our starting point is a 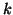 -step
Lanczos factorization (4.10):
-step
Lanczos factorization (4.10):
where
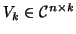 has orthonormal columns,
has orthonormal columns,
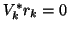 ,
and
,
and
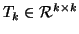 is real, symmetric, and tridiagonal
with nonnegative subdiagonal elements.
The columns of
is real, symmetric, and tridiagonal
with nonnegative subdiagonal elements.
The columns of 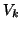 are referred to as the Lanczos vectors.
For implicit restart it is important that
the columns of
are referred to as the Lanczos vectors.
For implicit restart it is important that
the columns of 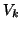 be made orthogonal to full accuracy.
be made orthogonal to full accuracy.
Subsections
Susan Blackford
2000-11-20
![]() has been
derived previously in §4.4.
Here, we discuss how to apply
implicit restart.
Our starting point is a
has been
derived previously in §4.4.
Here, we discuss how to apply
implicit restart.
Our starting point is a ![]() -step
Lanczos factorization (4.10):
-step
Lanczos factorization (4.10):