




Next: Implementation of Locking and
Up: Orthogonal Deflating Transformation
Previous: Purging .
Contents
Index
The deflating orthogonal transformation construction shown
in Algorithm 4.9 is
clearly stable (i.e., a componentwise relatively accurate representation of
the transformation one would obtain in exact arithmetic). There is
no question that the similarity transformation 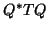 preserves the eigenvalues of
preserves the eigenvalues of 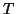 to full numerical accuracy.
However, there is a serious
question about how well
the tridiagonal form is preserved
during locking and/or purging. A modification to the basic
algorithm is needed to assure that if
to full numerical accuracy.
However, there is a serious
question about how well
the tridiagonal form is preserved
during locking and/or purging. A modification to the basic
algorithm is needed to assure that if
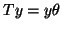 ,
then
,
then
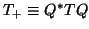 is symmetric and numerically tridiagonal
(i.e., the entries outside the tridiagonal band are all tiny relative
to
is symmetric and numerically tridiagonal
(i.e., the entries outside the tridiagonal band are all tiny relative
to 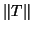 ).
).
The fact that 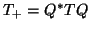 is
tridiagonal depends upon the term
is
tridiagonal depends upon the term 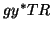 vanishing in the expression
vanishing in the expression
However, on closer examination, we see that
where 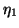 is the first component of
is the first component of 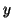 . Therefore,
. Therefore,
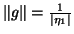 .
So there may be numerical difficulty when the first component of
.
So there may be numerical difficulty when the first component of 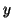 is small. To be specific,
is small. To be specific,
 and
thus
and
thus 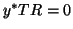 in exact arithmetic. However, in finite
precision, the computed
in exact arithmetic. However, in finite
precision, the computed
 .
The error
.
The error 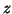 will be on the order of
will be on the order of 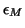 relative to
relative to 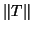 ,
but
,
but
so this term may be quite large. It may be as large as order 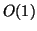 if
if
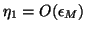 .
This is of serious concern and will occur in practice without the modification
we now propose.
.
This is of serious concern and will occur in practice without the modification
we now propose.
The remedy is to introduce a step-by-step acceptable perturbation and
rescaling of the vector 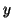 to simultaneously force the conditions
to simultaneously force the conditions
to hold with sufficient accuracy in finite precision.
To accomplish this, we shall devise a scheme to achieve
numerically. As shown in [420], this modification is sufficient to
establish
 numerically, relative to
numerically, relative to 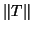 for
for 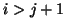 .
.
The basic idea is as follows: If, at the 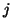 th step, the computed
quantity
th step, the computed
quantity
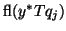 is not sufficiently small, it is adjusted
to be small enough by scaling the vector
is not sufficiently small, it is adjusted
to be small enough by scaling the vector 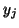 with a number
with a number 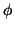 and the component
and the component 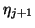 with a number
with a number 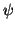 .
With this rescaling just prior to the computation of
.
With this rescaling just prior to the computation of 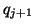 , we
have
, we
have
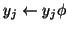 and
and
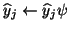 ,
where
,
where
![$y^* = [ y_j^* , \hat{y}_j^*]$](img1089.png) .
Certainly,
.
Certainly, 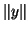 should not be altered with this scaling and this
is therefore required.
This gives the following system of equations to determine
should not be altered with this scaling and this
is therefore required.
This gives the following system of equations to determine 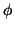 and
and 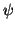 : If
: If
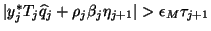 ,
(_j )^2 + (1 - _j^2)^2 &=& 1,
,
(_j )^2 + (1 - _j^2)^2 &=& 1,
y_j^* T_j q_j + _j _j _j+1 &=&
_M _j+1.
If 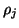 is on the order of
is on the order of
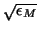 , the scaling
may be absorbed into
, the scaling
may be absorbed into 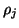 without alteration of
without alteration of 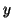 and also
without affecting the numerical orthogonality of
and also
without affecting the numerical orthogonality of 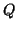 .
When
.
When 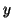 is modified, it turns out that none of the previously
computed
is modified, it turns out that none of the previously
computed
 need to be altered.
After step
need to be altered.
After step 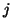 , the vector
, the vector 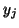 is simply rescaled in subsequent steps, and
the formulas defining
is simply rescaled in subsequent steps, and
the formulas defining
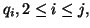 are invariant with respect to scaling of
are invariant with respect to scaling of 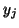 .
For complete detail, one should consult [420].
.
For complete detail, one should consult [420].
Algorithm 4.10 implements this scheme
to compute an acceptable 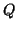 .
.![[*]](http://www.netlib.org/utk/icons/footnote.png) In practice, this transformation may
be computed and applied in place to obtain a
In practice, this transformation may
be computed and applied in place to obtain a
 and
and
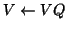 without storing
without storing 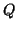 . However, that implementation
is quite subtle and the construction of
. However, that implementation
is quite subtle and the construction of 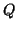 is obscured by the details
required to avoid additional storage.
This code departs slightly from the above description since the
vector
is obscured by the details
required to avoid additional storage.
This code departs slightly from the above description since the
vector 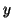 is rescaled to have unit norm only after all of
the columns
is rescaled to have unit norm only after all of
the columns 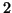 to
to 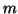 have been determined.
have been determined.

There are several implementation issues.
- (3)
- The perturbation
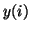 shown here avoids problems with exact zero initial entries in
the eigenvector
shown here avoids problems with exact zero initial entries in
the eigenvector 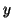 . In theory, this should not happen when
. In theory, this should not happen when 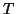 is unreduced
but it may happen numerically if
is unreduced
but it may happen numerically if 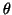 is weakly represented in
the starting vector.
There is a cleaner implementation possible that does not modify zero entries.
This is the simplest (and crudest) correction.
is weakly represented in
the starting vector.
There is a cleaner implementation possible that does not modify zero entries.
This is the simplest (and crudest) correction.
- (10)
- As soon as
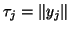 is sufficiently large, there is no need for
any further corrections. Deleting this if-clause reverts to the unmodified
calculation of
is sufficiently large, there is no need for
any further corrections. Deleting this if-clause reverts to the unmodified
calculation of 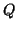 shown in Algorithm 4.9.
shown in Algorithm 4.9.
- (16)
- This shows one of several possibilities for modifying
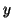 to achieve
the desired goal of numerically tiny elements outside the
tridiagonal band of
to achieve
the desired goal of numerically tiny elements outside the
tridiagonal band of 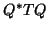 . More sophisticated strategies would
absorb as much of the scaling as possible into the diagonal element
. More sophisticated strategies would
absorb as much of the scaling as possible into the diagonal element
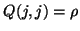 . Here, the branch that does scale
. Here, the branch that does scale 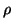 instead
of
instead
of 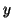 is designed so that
is designed so that
 .
.





Next: Implementation of Locking and
Up: Orthogonal Deflating Transformation
Previous: Purging .
Contents
Index
Susan Blackford
2000-11-20
![]() is
tridiagonal depends upon the term
is
tridiagonal depends upon the term ![]() vanishing in the expression
vanishing in the expression
![]() to simultaneously force the conditions
to simultaneously force the conditions
![]() th step, the computed
quantity
th step, the computed
quantity
![]() is not sufficiently small, it is adjusted
to be small enough by scaling the vector
is not sufficiently small, it is adjusted
to be small enough by scaling the vector ![]() with a number
with a number ![]() and the component
and the component ![]() with a number
with a number ![]() .
With this rescaling just prior to the computation of
.
With this rescaling just prior to the computation of ![]() , we
have
, we
have
![]() and
and
![]() ,
where
,
where
![]() .
Certainly,
.
Certainly, ![]() should not be altered with this scaling and this
is therefore required.
This gives the following system of equations to determine
should not be altered with this scaling and this
is therefore required.
This gives the following system of equations to determine ![]() and
and ![]() : If
: If
![]() ,
(_j )^2 + (1 - _j^2)^2 &=& 1,
,
(_j )^2 + (1 - _j^2)^2 &=& 1,
![]() is on the order of
is on the order of
![]() , the scaling
may be absorbed into
, the scaling
may be absorbed into ![]() without alteration of
without alteration of ![]() and also
without affecting the numerical orthogonality of
and also
without affecting the numerical orthogonality of ![]() .
When
.
When ![]() is modified, it turns out that none of the previously
computed
is modified, it turns out that none of the previously
computed
![]() need to be altered.
After step
need to be altered.
After step ![]() , the vector
, the vector ![]() is simply rescaled in subsequent steps, and
the formulas defining
is simply rescaled in subsequent steps, and
the formulas defining
![]() are invariant with respect to scaling of
are invariant with respect to scaling of ![]() .
For complete detail, one should consult [420].
.
For complete detail, one should consult [420].
![]() .
.![]() In practice, this transformation may
be computed and applied in place to obtain a
In practice, this transformation may
be computed and applied in place to obtain a
![]() and
and
![]() without storing
without storing ![]() . However, that implementation
is quite subtle and the construction of
. However, that implementation
is quite subtle and the construction of ![]() is obscured by the details
required to avoid additional storage.
This code departs slightly from the above description since the
vector
is obscured by the details
required to avoid additional storage.
This code departs slightly from the above description since the
vector ![]() is rescaled to have unit norm only after all of
the columns
is rescaled to have unit norm only after all of
the columns ![]() to
to ![]() have been determined.
have been determined.