




Next: Orthogonal Deflating Transformation
Up: Implicitly Restarted Lanczos Method
Previous: Computational Costs and Tradeoffs
Contents
Index
Deflation and Stopping Rules
Deflation is an important concept in the practical implementation
of the QR iteration and therefore equally important to the IRLM.
In the context of the QR iteration, deflation amounts to setting
a small subdiagonal (and corresponding superdiagonal) element of the
tridiagonal matrix 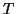 to zero. This is called deflation because
it splits the tridiagonal matrix into two smaller subproblems which
may be independently refined further.
to zero. This is called deflation because
it splits the tridiagonal matrix into two smaller subproblems which
may be independently refined further.
However, in the context of IRLM,
the usual QR deflation techniques are
not always appropriate. Additional deflation capabilities specific to
implicit restart are needed.
It is often desirable to deflate at a coarser accuracy
level 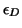 with
with
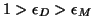 ,
where
,
where 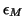 is machine precision.
In theory (i.e., in
exact arithmetic), when
is machine precision.
In theory (i.e., in
exact arithmetic), when  has multiple eigenvalues it would be
impossible for IRLM to compute more than one eigenvector to such
a multiple eigenvalue.
This is because it is a ``single vector" rather than a block method.
However, in practice, there is usually little difficulty in computing
multiple eigenvalues, because the method deflates itself as convergence
takes place, and roundoff usually introduces components in new eigenvector directions
in the subsequent starting vectors. Nevertheless, this can be unreliable
and miss a multiple eigenvalue. In any case, this approach typically
will require a stringent convergence tolerance in order to find all
instances of a multiple eigenvalue.
has multiple eigenvalues it would be
impossible for IRLM to compute more than one eigenvector to such
a multiple eigenvalue.
This is because it is a ``single vector" rather than a block method.
However, in practice, there is usually little difficulty in computing
multiple eigenvalues, because the method deflates itself as convergence
takes place, and roundoff usually introduces components in new eigenvector directions
in the subsequent starting vectors. Nevertheless, this can be unreliable
and miss a multiple eigenvalue. In any case, this approach typically
will require a stringent convergence tolerance in order to find all
instances of a multiple eigenvalue.
It is far more efficient to deflate (i.e., lock) an approximate
eigenvalue once it has converged to a certain level of accuracy and
to force subsequent Lanczos vectors to be orthogonal to the
converged subspace. With this capability, additional instances of a
multiple eigenvalue can be computed to the same specified accuracy
without the expense of forcing them to converge to unnecessarily high
accuracy.
In the Lanczos process, as with a QR iteration, it is possible
for some of the
leading 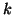 subdiagonals to become small during the course of implicit
restart. However, it is usually the case that there are converged
Ritz values appearing in the spectrum of
subdiagonals to become small during the course of implicit
restart. However, it is usually the case that there are converged
Ritz values appearing in the spectrum of 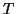 long before small
subdiagonal elements appear. This convergence is usually detected
through observation of a small last component in an eigenvector
long before small
subdiagonal elements appear. This convergence is usually detected
through observation of a small last component in an eigenvector 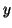 of
of 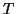 .
When this happens, we are able to construct
an orthogonal similarity transformation of
.
When this happens, we are able to construct
an orthogonal similarity transformation of 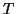 that will give
an equivalent Lanczos factorization with a slightly perturbed
that will give
an equivalent Lanczos factorization with a slightly perturbed 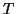 that
does indeed have a zero subdiagonal, and this is the basis of our
deflation scheme.
that
does indeed have a zero subdiagonal, and this is the basis of our
deflation scheme.
In the context of IRLM, there are two types of deflation required:
- Locking:
- If a Ritz value
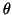 has converged
(meaning
has converged
(meaning
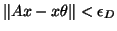 ) and is thought to be a member
of the wanted set of eigenvalues, we wish to declare
it converged, decouple the eigenpair
) and is thought to be a member
of the wanted set of eigenvalues, we wish to declare
it converged, decouple the eigenpair  , and continue
to compute remaining eigenvalues with no further alteration of
, and continue
to compute remaining eigenvalues with no further alteration of 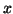 or
or 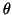 .
This process is called locking.
.
This process is called locking.
- Purging:
- If a Ritz value
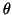 has converged but
is not a member of the wanted set, we wish to
decouple and remove the eigenpair
has converged but
is not a member of the wanted set, we wish to
decouple and remove the eigenpair  from the current Krylov subspace spanned by the Lanczos vectors.
This process is called purging.
from the current Krylov subspace spanned by the Lanczos vectors.
This process is called purging.
Techniques for this deflation were first developed
in [289,294]. The scheme we present here is based on
an improvement developed in [420].
This scheme allows for stable and efficient deflation (or locking) of Ritz
values that have converged with a specified
relative accuracy of 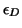 which may be considerably larger than
machine
precision
which may be considerably larger than
machine
precision 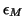 . This is particularly important when a
SI is not available to accelerate convergence.
Typically in this setting the number of matrix-vector products will
be large, and it will be highly desirable to lock converged Ritz values
at low tolerances. This will avoid the expense of the matrix-vector products
that would be required to achieve an accuracy that would allow normal
QR-type deflation. Also, it is important to be able to purge
converged but unwanted Ritz values. As pointed out in [289],
the forward instability of the QR bulge chase process
discovered by Parlett and Le [359] will prevent implicit
restart being used for purging converged unwanted Ritz values.
. This is particularly important when a
SI is not available to accelerate convergence.
Typically in this setting the number of matrix-vector products will
be large, and it will be highly desirable to lock converged Ritz values
at low tolerances. This will avoid the expense of the matrix-vector products
that would be required to achieve an accuracy that would allow normal
QR-type deflation. Also, it is important to be able to purge
converged but unwanted Ritz values. As pointed out in [289],
the forward instability of the QR bulge chase process
discovered by Parlett and Le [359] will prevent implicit
restart being used for purging converged unwanted Ritz values.





Next: Orthogonal Deflating Transformation
Up: Implicitly Restarted Lanczos Method
Previous: Computational Costs and Tradeoffs
Contents
Index
Susan Blackford
2000-11-20
![]() with
with
![]() ,
where
,
where ![]() is machine precision.
In theory (i.e., in
exact arithmetic), when
is machine precision.
In theory (i.e., in
exact arithmetic), when ![]() has multiple eigenvalues it would be
impossible for IRLM to compute more than one eigenvector to such
a multiple eigenvalue.
This is because it is a ``single vector" rather than a block method.
However, in practice, there is usually little difficulty in computing
multiple eigenvalues, because the method deflates itself as convergence
takes place, and roundoff usually introduces components in new eigenvector directions
in the subsequent starting vectors. Nevertheless, this can be unreliable
and miss a multiple eigenvalue. In any case, this approach typically
will require a stringent convergence tolerance in order to find all
instances of a multiple eigenvalue.
has multiple eigenvalues it would be
impossible for IRLM to compute more than one eigenvector to such
a multiple eigenvalue.
This is because it is a ``single vector" rather than a block method.
However, in practice, there is usually little difficulty in computing
multiple eigenvalues, because the method deflates itself as convergence
takes place, and roundoff usually introduces components in new eigenvector directions
in the subsequent starting vectors. Nevertheless, this can be unreliable
and miss a multiple eigenvalue. In any case, this approach typically
will require a stringent convergence tolerance in order to find all
instances of a multiple eigenvalue.
![]() subdiagonals to become small during the course of implicit
restart. However, it is usually the case that there are converged
Ritz values appearing in the spectrum of
subdiagonals to become small during the course of implicit
restart. However, it is usually the case that there are converged
Ritz values appearing in the spectrum of ![]() long before small
subdiagonal elements appear. This convergence is usually detected
through observation of a small last component in an eigenvector
long before small
subdiagonal elements appear. This convergence is usually detected
through observation of a small last component in an eigenvector ![]() of
of ![]() .
When this happens, we are able to construct
an orthogonal similarity transformation of
.
When this happens, we are able to construct
an orthogonal similarity transformation of ![]() that will give
an equivalent Lanczos factorization with a slightly perturbed
that will give
an equivalent Lanczos factorization with a slightly perturbed ![]() that
does indeed have a zero subdiagonal, and this is the basis of our
deflation scheme.
that
does indeed have a zero subdiagonal, and this is the basis of our
deflation scheme.