As we shall see, from the standpoint of data access, the left-looking variant is better than the right-looking variant. To begin, we assume that
and that we wish to advance the factorization to the form
Comparing Eqs. 8 and 9 we see that the factorization is advanced by first solving the triangular system
and then performing a matrix-matrix product to update the rest of the middle block column of U,
Next we perform the factorization
and lastly the pivoting
Observe that data accesses all occur to the left of the block column being updated. Moreover, the only write access occurs within this block column. Matrix elements to the right are referenced only for pivoting purposes, and even this procedure may be postponed until needed with a simple rearrangement of the above operations.
In evaluating the I/O cost for the left-looking out-of-core LU factorization algorithm two variants of the left-looking algorithm will be considered. In the first we always store the matrix on disk in unpivoted form at all intermediate phases of the algorithm, writing out the whole matrix in pivoted form only in the last step of the algorithm. In this case pivoting has to be done ``on the fly'' when matrix blocks are read in from disk. In the second version of the algorithm the matrix is stored on disk in pivoted form.
Consider the version in which the matrix is stored in unpivoted form.
Whenever a block is read in the whole 
block must be read so
that it can be pivoted. Upon completion of a step the newly-factored block
is the only block that is written to disk, except in the last step in which
we write out all blocks in pivoted form so that the final matrix stored
on disk is pivoted (although in some cases these writes may be omitted if
an unpivoted matrix is called for - the pivots can always be applied
later since they are stored in the pivot vector). At some general
step k of the algorithm the I/O cost is
where the first term corresponds to reading and writing the block to be factored in this step and the second term to reading in the blocks to the left. Summing over k and adding in the time to write out all pivoted blocks in the last step, the total cost for this version of the left-looking algorithm is
Thus, to order 
the time to do the writes can be ignored. If we assume
that reads and writes take approximately the same time (i.e., 
),
then comparison with Eq. 7 shows that this version of
the left-looking algorithm should perform less I/O than the right-looking
algorithm.
Now consider the version of the left-looking algorithm in which blocks
are always stored on disk in pivoted form. In this case it is no longer
necessary to read in all rows of an block, but it is necessary
to write out partial blocks in each step. This is because the pivoting
performed in the factorization
of the block column must also be applied to the blocks to the left, which
must then be written to disk.
In some general step k all of
the block to be updated must be read in and written out. The parts of the
blocks to the left that must be read in form a stepped trapeziodal shape
(see Figure 2(a)), while the
parts of the blocks to the left that must
be written out after applying the pivots for this step form a rectangle
(see Figure 2(b)). Thus for step k>0 the I/O cost is
and for step k=0 the I/O cost is 
. Thus, the total I/O cost is
It is interesting to note that if reads and writes take the same time the two left-looking versions of the algorithm have the same I/O cost, and they both have a lower I/O cost than the right-looking algorithm. We therefore expect a left-looking algorithm to be better than a right-looking algorithm for out-of-core LU factorization.
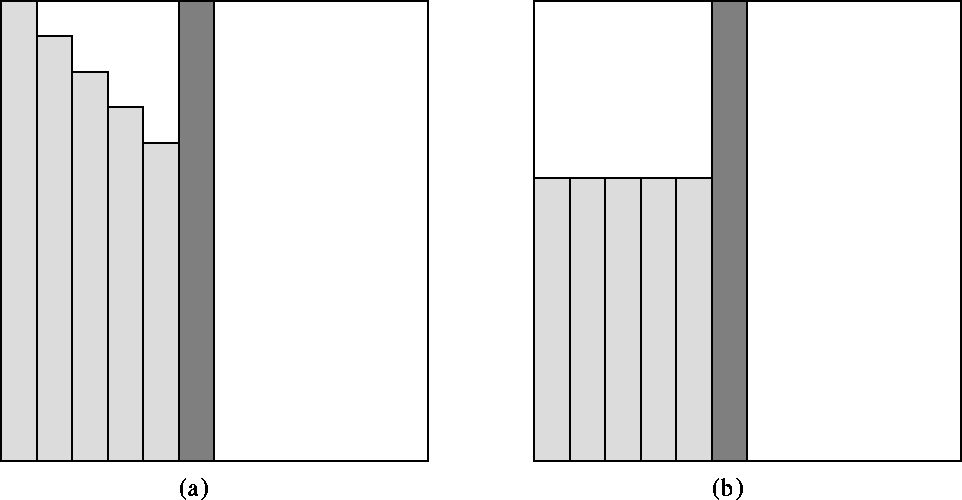
Figure: This figure pertains to the left-looking LU factorization
algorithm that stores the matrix in pivoted form.
(a) The shaded blocks show the block columns read from disk in
step k=5. The dark shaded block is the block being updated in this step.
(b) The shaded blocks show the block columns written to disk in
step k=5.
