In this section the implementation of the sequential, left-looking, out-of-core LU factorization routine will be discussed. As we shall see in Section 6, once the sequential version has been implemented it is a relatively easy task to parallelize it using the BLACS, PBLAS, and ScaLAPACK, and the parallel out-of-core routines described in Section 5.
In the out-of-core algorithm only two block columns of width 
may be in-core at any
time. One of these is the block column being updated and factored which
we shall refer to as the active block. The other is one of the
block columns lying to the left of the active block column which we shall
refer to as a temporary block.
As we saw in Section 2.2, the three main computational
tasks in a step of the left-looking algorithm are a triangular
solve (Eq. 10), a matrix-matrix multiplication
(Eq. 11), and an LU factorization (Eq. 12).
In the out-of-core algorithm the triangular solve and matrix-matrix
multiplication steps are intermingled so that a temporary block can play its
part in both of these operations but be read only once. To clarify this,
consider the role that block column i plays in the factorization of
block column k (where i<k). In Figure 3, the first i rows of
block column i play no role in factoring block column k. The lower
triangular
portion of the next rows of
block column i are labeled 
, and the next 
rows are
labeled 
.
The last M-k rows are labeled D. The corresponding portions of
block column k are labeled 
, 
, and E. Then the part played by
block column
i in factoring block column k can be expressed in the following three
operations,
where in Eqs. 19 and 20 we use the
given by Eq. 18. It should be noted that
Eqs. 19 and 20 can be combined in a single
matrix-matrix multiplication operation
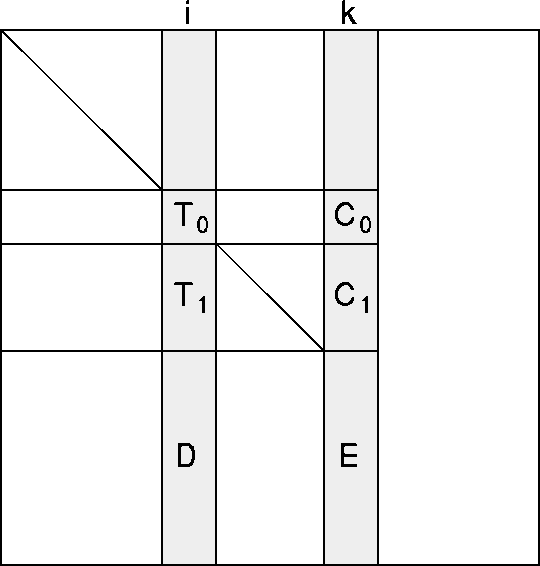
Figure: Partitioning of temporary block i and active block k.
In updating block column k, the out-of-core algorithm sweeps over all block columns to the left of block column k and performs for each the triangular solve in Eq. 18 and the matrix-matrix multiplication in Eq. 21. After all the block columns to the left of the block have been processed in this way using the Level 3 BLAS routines _TRSM and _GEMM [6], the matrix E is then factored using the LAPACK routine _GETRF [1].
If the matrix is stored on disk without applying the pivots to it, then whenever a block column is read in the pivots found up to that point must be applied to it using _LASWP, an LAPACK auxiliary routine. Also after updating and factoring the active block, the pivots must be applied to it in reverse order to undo the effect of pivoting before storing the block column to disk. In this version of the left-looking algorithm complete block columns are always read or written. In the version of the algorithm in which the matrix is stored on disk in pivoted form it is necessary to read in only those parts of the temporary blocks that play a role in the computation. When a partial temporary block is read in the pivots found when factoring E in the previous step must be applied before using it, and it must then be written back out to disk.
In Figure 4 the pseudocode is presented for the version of
the left-looking algorithm in which the matrix is stored in unpivoted
form. Since a vector of pivot information is maintained in-core, the
factored matrix can always be read in later to be pivoted.
It has been assumed in Figure 4 that the matrix is
and that M is divisible by the block size . However,
the general case is scarcely more complicated.
It should be noted that it is necessary to position the file pointer
(at the start of the file) only once in each pass through the outer loop.
Figure: Pseudocode for out-of-core, left-looking LU factorization algorithm
that leaves matrix in unpivoted form.
