Although in section 2 we saw that the left-looking LU
factorization routine has a lower I/O cost that the right-looking variant,
the left-looking algorithm has less inherent parallelism since it acts only
on single blocks. We therefore propose a hybrid parallel algorithm in
which a single block actually spans several widths of the process grid, say 
.
In effect, the matrix is now blocked at two levels. It is divided into
blocks of size 
elements, which are distributed cyclicly over the
process grid, but we apply the left-looking algorithm to
``superblocks'' of width 
columns where the process grid is assumed
to be of size 
. If is chosen large enough we have a
pure right-looking algorithm, and if and Q are both 1 we essentially
recover the pure left-looking algorithm. Within a superblock
we use a right-looking LU factorization algorithm (P_GETRF) to get good
parallelism, but at the superblock level we employ a left-looking
algorithm to control I/O costs. The parameter can be used
to trade off parallelism and I/O cost.
In Figure 7 we show an example for a 
process
grid, and 
. For clarity we consider here a matrix consisting of
only four column superblocks, though
in a ``real'' application we would expect the number to be much larger.
In Figure 7 the first two superblocks have been factored,
while the third and fourth superblocks have not yet been changed. We now
consider the next stage of the algorithm in which
the third superblock, for which the data distribution is shown
explicitly, is factored. Note that each of the small numbered
squares is actually an 
block, with the numbering indicating
the position in the process grid to which it is assigned. At the end of
this stage of the algorithm the first three superblocks will have been
factored, and the fourth will still be unchanged. In the following we shall
refer to the superblock being factored as the active superblock.
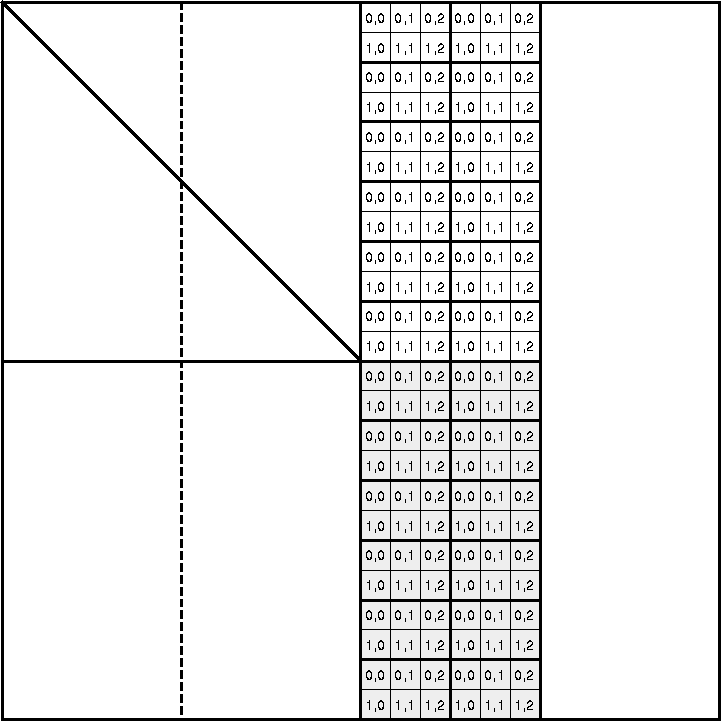
Figure: Schematic view of the parallel hybrid out-of-core algorithm for
the case 
and .
The parallel implementation closely follows the sequential implementation presented in Section 3. Block columns are read and written using the routines P_READ and P_WRITE. The file pointer is positioned with P_GSEEK. These routines are part of the BLAPIO library introduced in Section 5. The triangular solve and matrix multiplication are done using PBLAS routines. Pivoting is performed by the ScaLAPACK auxiliary routine P_LAPIV, while the factorization is done by the ScaLAPACK routine P_GETRF. Since all these routines reference matrices as global data structures, parallelization of the sequential algorithm is almost trivial. Pseudocode for the parallel version is given in Figure 8.
Figure: Pseudocode for parallel, out-of-core, left-looking LU factorization
algorithm that leaves matrix in unpivoted form.