In this section some preliminary performance results are presented for the parallel left-looking LU factorization algorithm running on an Intel Paragon concurrent computer. These results are intended to illustrate a few general points about the performance of the algorithms used, and do not constitute a detailed performance study. In the work presented here we were constrained by difficulties encountered in getting exclusive access to the Paragon for sufficiently long periods. In addition we found that the parallel file system of the Paragon to which we had access was close to full much of the time. We hope to overcome these problems in the future and undertake a detailed performance study in future work. All the runs were made in exclusive use mode, i.e., with logins disabled to prevent other users accessing the system. This was done because the performance of PFS is affected by the load on the service nodes, even if other users are just editing or compiling.
The first runs were done using the version of the algorithm that maintains
the partially factored matrix in unpivoted form throughout the algorithm.
Timing results are shown for 
and 
process meshes
in Tables 1 and
2 for a distributed out-of-core matrix. In these cases
we say that the matrix was both logically and physically distributed because
each processor opens a separate file.
As expected for this version of the algorithm, the time spent writting to
PFS is much less than the time spent reading. However, the most striking
aspect of the timings is the fact that pivoting dominates.
The large amount of time spent pivoting arises because each time a superblock
is read in all the pivots evaluated so far must be applied to it.
For a sequential algorithm (i.e., 
), a total of
superblocks of width 
elements must be pivoted. Thus,
pivoting entails 
exchanges of elements, which is of the
same order as the I/O cost. In the parallel case, we must replace by the
width of a superblock, 
. Thus, in order for the version of the
algorithm that stores the matrix in unpivoted form to be asymptotically
faster than the version that stores the matrix in pivoted form we require
where W and R are the costs of writing and reading an element, respectively, and P is the cost of pivoting an element.
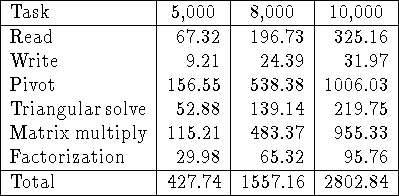
Table: Timings in seconds for the main phases of out-of-core LU
factorization of 
matrices. Results are shown for M=5000,
8000 and 10000. In all cases 
, 
, P=4, and Q=4.
The version of the algorithm that stores the matrix in unpivoted form and
performs pivoting on the fly was used.
The out-of-core matrix was physically and logically distributed.
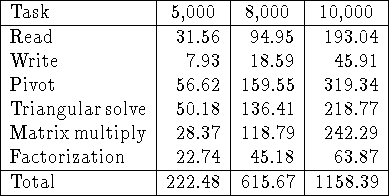
Table: Timings in seconds for the main phases of out-of-core LU
factorization of matrices. Results are shown for M=5000,
8000 and 10000. In all cases , , P=8, and Q=8.
The version of the algorithm that stores the matrix in unpivoted form and
performs pivoting on the fly was used.
The out-of-core matrix was physically and logically distributed.
In general, there is no reason why writing should be substantially faster
then reading, so we would not expect Eq. 22 to hold. Thus,
the version of the algorithm that stores the matrix in pivoted form is
expected to be faster. This is borne out by the timings presented in
Table 3 for an process mesh. These timings are
directly comparable with those of Table 2, and show
that the version of the algorithm that stores the matrix in
pivoted form is faster by 10-15%. Note that the
time for writing is slightly more than half the time for reading, suggesting
that it takes slightly longer to write a superblock than to read it.
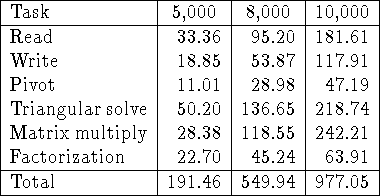
Table: Timings in seconds for the main phases of out-of-core LU
factorization of matrices. Results are shown for M=5000,
8000 and 10000. In all cases , , P=8, and Q=8.
The version of the algorithm that stores the matrix in pivoted form was used.
The out-of-core matrix was physically and logically distributed.
We next attempted to investigate the effect of varying the width of the
superblock by increasing 
from 2 to 10. The results are shown
in Table 4. A problem will fit in core if
the memory required in each process
to hold two superblocks exceeds that required to hold the entire matrix, i.e.,
if
or 
. Thus, for the parameters of Table 4
the M=5000 and M=8000 cases fit in core, so we just read in the whole
matrix, factorize it using the standard ScaLAPACK routine
P_GETRF, and then write it out again. In Table 4
it takes about 58 seconds to perform an in-core factorization of a
matrix, compared with 191 seconds for an out-of-core
factorization (see table 3). The M=8000 case in
Table 4 failed, presumably because PFS was not able to
handle the need to simultaneously read 8 Mbytes from each of
64 separate files. The M=10000 case ran successfully out-of-core, and
the results in Table 4 should be compared with those
in Table 3, from which we observe that increasing
increases the time for I/O and factorization, but decreases the times for all
other phases of the algorithm. The increase in I/O is an unexpected result
since increasing should decrease the I/O cost. Perhaps the larger
value of increases the I/O cost because larger amounts of data are
being read and written, leading to congestion in the parallel I/O system.
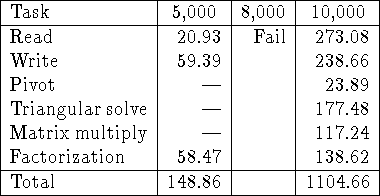
Table: Timings in seconds for the main phases of out-of-core LU
factorization of matrices. Results are shown for M=5000,
8000 and 10000. In all cases , 
, P=8, and Q=8.
The version of the algorithm that stores the matrix in pivoted form was used.
Note that the M=5000 and 8000 cases ran in-core, and that the
M=8000 case failed.
The out-of-core matrix was physically and logically distributed.
To understand the effect of varying the superblock width on the time for the triangular solve, matrix multiplication, and factorization phases of the algorithm we derive the following expressions for the number of floating-point operations in each phase,
These expressions apply in the sequential case ( 
), but the
corresponding expression for the parallel algorihm is obtained by
replacing by 
.
It should be noted that the total floating-point operation count for
all three computational phases is 
, but the above expressions show
that the way these operations are distributed among the phases depends on the
width of the superblock, .
Thus, an increase in the superblock width results in an increase in the
factorization time, and a decrease in the time for matrix multiplication. If
the superblock width is sufficiently small compared with the matrix size
then a small increase results in an increase in the triangular solve
time. However, if the superblock width is large an increase will decrease
the triangular solve time. It should be remembered that all three of these
phases are running in parallel so communication time also influences
the total running time. In general, increasing the or should
decrease communication time on the Paragon as data are communicated in
larger blocks. If the times for the computational phases in Tables
3 and 4 are summed we get
about 524 seconds for and about 432 seconds for which suggests
that a larger value of results in more efficient parallel compputation
overall. Communication overhead, together with the floating-point operation
count, determines the performance of the computational phases of the algorithm
as changes.
The failure of the M=8000 case in Table 3 prompted us to devise a second way of implementing logically distributed files. Instead of opening a separate file for each process, the new method opens a single file and divides it into blocks, assigning one block to each process. This does not change the user interface to the BLAPIOS described in Sec. 5. We refer to this type of file as a physically shared, logically distributed file. It should be noted that the terms ``physically shared'' and ``physically distributed'' refer to the view of the parallel file system from within the BLAPIOS. At the hardware level the file, or files, may be striped across multiple disks, as is the case for the Intel Paragon.
The rest of the results presented in this section are for physically
shared, logically distributed files, and the version of the algorithm that
stores the matrix in pivoted form. In Tables 5 and
6 results are presented for the same problems on
and process meshes. It is interesting to note
that increasing the number of processors from 16 to 64 results in only
a very small decrease in the time for the triangular solve phase, indicating
that the parallel efficiency for this phase is low. This is in contrast
with the matrix multiplication phase which exhibits almost perfect speedup.
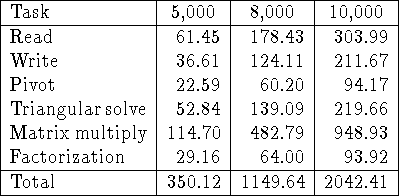
Table: Timings in seconds for the main phases of out-of-core LU
factorization of matrices. Results are shown for M=5000,
8000 and 10000. In all cases , , P=4, and Q=4.
The version of the algorithm that stores the matrix in pivoted form was used.
The out-of-core matrix was logically distributed, but physically shared.
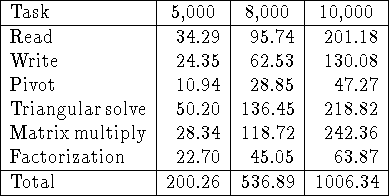
Table: Timings in seconds for the main phases of out-of-core LU
factorization of matrices. Results are shown for M=5000,
8000 and 10000. In all cases , , P=8, and Q=8.
The version of the algorithm that stores the matrix in pivoted form was used.
The out-of-core matrix was logically distributed, but physically shared.
In Table 7 timings are presented for the case
for an process mesh. Comparing these results first with
those given in Table 4 for a physically and
logically distributed file, the decrease in the times for reading and writing
is striking. Secondly, of course, the physically shared case no longer
fails for the M=8000 in-core case. Comparison between Tables
6 and 7 shows that a for physically
shared file an increase in results in a decrease in I/O time, as
expected from the dependency of the I/O time on 
. However, the
decrease is less than the expected factor of 5, particularly for the writes.
Results in Table 8 for the case 
show a read
time for the M=10000 case which is about the same as for , and
a write time that is substantially less. This again shows that as
increases, thereby increasing the amount of data being read and written
in each I/O operation, I/O performance starts to degrade quite
significantly once is sufficiently large.
Table 8 shows timings for the M=10000 case for the same
problem parameters as in Table 7, but for . Comparing
the results in Tables 6, 7, and
8 we see that the time for writing data does not
decrease montonically as increase, but is smallest for . Again
we ascribe this behavior to the apparent degradation in I/O performance
when the volume of simultaneous I/O is large.
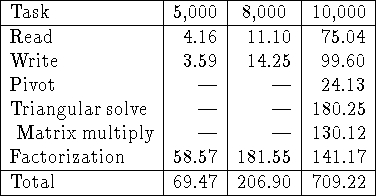
Table: Timings in seconds for the main phases of out-of-core LU
factorization of matrices. Results are shown for M=5000,
8000 and 10000. In all cases , , P=8, and Q=8.
The version of the algorithm that stores the matrix in pivoted form was used.
Note that the M=5000 and 8000 cases ran in-core.
The out-of-core matrix was logically distributed, but physically shared.
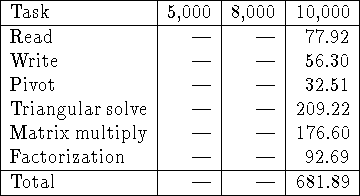
Table: Timings in seconds for the main phases of out-of-core LU
factorization of matrices. Results are shown for
M=10000 with , , P=8, and Q=8.
The version of the algorithm that stores the matrix in pivoted form was used.
The out-of-core matrix was logically distributed, but physically shared.
