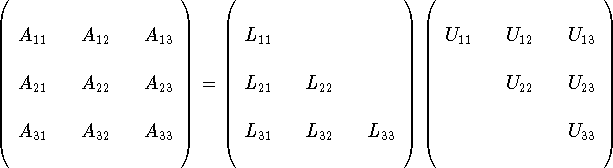
Let us consider the decomposition of the matrix A into its LU factorization with the matrix partitioned in the following way. Let us suppose that we have factored A as A = LU. We write the factors in block-partitioned form and observe the consequences.
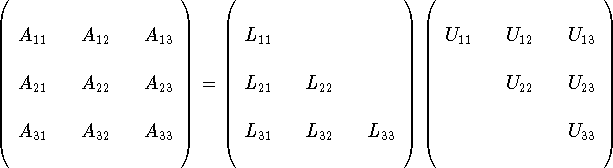
Multiplying L and U together and equating terms with A, we have
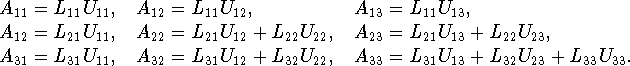
With these simple relationships we can develop variants by postponing the formation of certain components and also by manipulating the order in which they are formed. A crucial factor for performance is the choice of the blocksize, k (i.e., the column width) of the second block column. A blocksize of 1 will produce matrix-vector algorithms, while a blocksize of k > 1 will produce matrix-matrix algorithms. Machine-dependent parameters such as cache size, number of vector registers, and memory bandwidth will dictate the best choice for the blocksize.
Two natural variants occur: right-looking and left-looking. (There are several other variants possible, we examine only two here.) The terms right and left refer to the regions of data access, as shown in Figure 1.
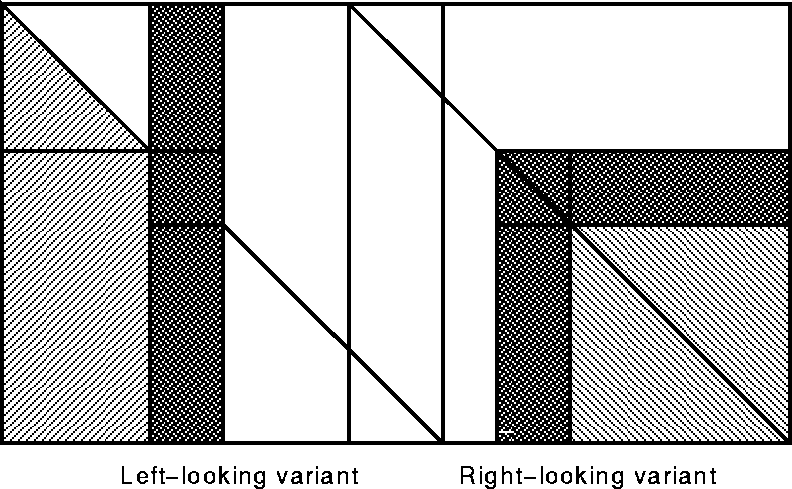
Figure: Memory access patterns for variants of LU decomposition.
The shaded parts indicate
the matrix elements accessed in forming a block row or column, and
the darker shading indicates the block row or column being modified.
The left-looking variant computes one block column at a time, using previously computed columns. The right-looking variant (the familiar recursive algorithm) computes a block row and column at each step and uses them to update the trailing submatrix. These variants have been called the i,j,k variants owing to the arrangement of loops in the algorithm. For a more complete discussion of the different variants, see [8, 13].
We now develop these block variants of LU factorization with partial pivoting.