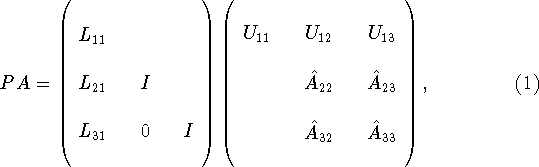
Suppose that a partial factorization of A has been obtained so that the first k columns of L and the first k rows of U have been evaluated. Then we may write the partial factorization in block partitioned form, with square blocks along the leading diagonal, as
where 
and 
are 
matrices, and
P is a permutation matrix representing the effects of pivoting.
Pivoting is performed to improve the numerical stability of the algorithm
and involves the interchange of matrix rows. The
blocks labeled 
in Eq. 1 are the updated
portion of A that has not yet been factored, and will be referred to as
the active submatrix.
We next advance the factorization by evaluating the next block column of L and the next block row of U, so that
where 
is a permutation matrix of order M-k. Comparing
Eqs. 1 and
2 we see that the factorization is advanced by first factoring the
first block column of the active submatrix which will be referred to as
the current column,
This gives the next block column of L. We then pivot the active submatrix to the right of the current column and the partial L matrix to the left of the current column,
and solve the triangular system
to complete the next block row of U. Finally, a matrix-matrix product is
performed to update 
,
Now, one simply needs to relabel the blocks to advance to the next block step.
The main advantage of the block partitioned form of the
LU factorization algorithm is that the updating of
(see Eq. 6)
involves a matrix-matrix operation if the block size is greater than 1.
Matrix-matrix operations generally perform more efficiently than matrix-vector
operations on high performance computers.
However, if the block size is equal to 1, then a matrix-vector operation is
used to perform an outer product -- generally the least efficient of
the Level 2 BLAS
[7] since it updates the whole submatrix.
Note that the original array A may be used to store the factorization, since the L is unit lower triangular and U is upper triangular. Of course, in this and all of the other versions of LU factorization, the additional zeros and ones appearing in the representation do not need to be stored explicitly.
We now derive the cost for performing I/O to and from disk for the
block-partitioned, right-looking LU factorization of an 
matrix A with a block size of 
. For clarity assume M is exactly
divisible by
. The factorization proceeds in 
steps which we shall index
. For some general step k, the active submatrix
is the 
matrix in the lower right corner of A, where
. In step k it is necessary to both read and write all of the
active submatrix, so the total I/O cost for the right-looking algorithm is
where R and W are the times to read and write one matrix element, respectively, and we assume there is no startup cost when doing I/O.
