




Next: An Improved Method
Up: 11 Load Balancing and
Previous: Applications and Extensions
C P maintained a significant activity in optimization.
There were several reasons for this, one of which
was, of course, natural curiosity. Another was the importance of load
balancing and data decomposition which is, as discussed previously in
this chapter, ``just'' an optimization problem. Again, we already
mentioned in Section 6.1 our interest in neural
networks as a naturally parallel approach to
artificial intelligence. Section 9.9 and Section 11.1 have
shown how neural networks can be used in a range of optimization
problems. Load balancing has the important (optimization)
characteristic of NP completeness, which implies that it would take an
exponential time to solve completely. Thus, we studied the travelling
salesman problem (TSP) which is well known to be NP-complete and
formally equivalent to other problems with this property. One
important contribution of C
P maintained a significant activity in optimization.
There were several reasons for this, one of which
was, of course, natural curiosity. Another was the importance of load
balancing and data decomposition which is, as discussed previously in
this chapter, ``just'' an optimization problem. Again, we already
mentioned in Section 6.1 our interest in neural
networks as a naturally parallel approach to
artificial intelligence. Section 9.9 and Section 11.1 have
shown how neural networks can be used in a range of optimization
problems. Load balancing has the important (optimization)
characteristic of NP completeness, which implies that it would take an
exponential time to solve completely. Thus, we studied the travelling
salesman problem (TSP) which is well known to be NP-complete and
formally equivalent to other problems with this property. One
important contribution of C P was the work of Simic
[Simic:90a;91a]. [Simic:91a]
P was the work of Simic
[Simic:90a;91a]. [Simic:91a]
Simic derived the relationship between the neural network
[Hopfield:86a] and elastic net [Durbin:87a;89a],
[Rose:90f;91a;93a],
[Yuille:90a]
approaches to the TSP. This work has been extensively reviewed
[Fox:91j;92c;92h;92i]
and we will not go into the details
here. A key concept is that of physical optimization which
implies the use of a physics approach of minimizing the energy, that
is, finding the ground state of a complex system
set up as a physical analogy to the optimization problem. This idea is
illustrated clearly by the discussion in Section 11.1.3 and
Section 11.2. One can understand some reasons why a physics
analogy could be useful from two possible plots of the objective
function to be minimized, against the possible configurations, that is,
against the values of parameters to be determined. Physical systems
tend to look like Figure 11.1(a), where correlated (i.e.,
local) minima are ``near'' global minima. We usually do not get the
very irregular landscape shown in Figure 11.1(b). In fact,
we do find the latter case with the so-called random field Ising model,
and here conventional physics methods perform poorly
[Marinari:92a], [Guagnelli:92a]. Ken Rose showed how these
ideas could be generalized to a wide class of optimization problems as
a concept called deterministic annealing [Rose:90f], [Stolorz:92a]. Annealing is
illustrated in Figure 11.23 (Color Plate). One uses temperature to
smooth out the objective function (energy function) so that at high
temperature one can find the (smeared) global minimum without getting
trapped in spurious local minima. Temperature is decreased skillfully
initializing the search at Temperature 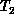 by the solution at the
previous higher temperature
by the solution at the
previous higher temperature 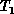 . This annealing can be applied
either statistically [Kirkpatrick:83a] as in Sections 11.1
and 11.3 or with a deterministic iteration. Neural and
elastic networks can be viewed as examples of deterministic annealing.
Rose generalized these ideas to clustering [Rose:90a;90c;91a;93a];
. This annealing can be applied
either statistically [Kirkpatrick:83a] as in Sections 11.1
and 11.3 or with a deterministic iteration. Neural and
elastic networks can be viewed as examples of deterministic annealing.
Rose generalized these ideas to clustering [Rose:90a;90c;91a;93a];
vector quantization used in coding [Miller:92b],
[Rose:92a]; tracking
[Rose:89b;90b]; and electronic packing [Rose:92b].
Deterministic annealing ;has also been used for robot path planning
with many degrees of freedom [Fox:90k], [Gandhi:90b] (see
also Figure 11.22 (Color Plate)), character recognition
[Hinton:92a], scheduling problems
[Gislen:89a;91a], [Hertz:92a],
[Johnston:92a], and quadratic assignment [Simic:91a].
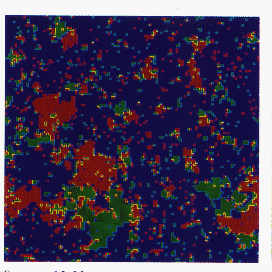
Figure 11.23: Annealing tracks global minima by
initializing search at one temperature by minima found at other temperatures .
Neural networks have been shown to perform poorly
in practice on the TSP [Wilson:88a], but we found them excellent
for the formally equivalent load-balancing problem in
Section 11.1. This is now understood from the fact that the
simple neural networks used in the TSP
[Hopfield:86a] used many redundant neural variables, and the
difficulties reported in [Wilson:88a] can be traced to the role of
the constraints that remove redundant variables. The neural network
approach summarized in Section 11.1.6 uses a parameterization that
has no redundancy and so it is not surprising that it works well. The
elastic network can be viewed as a neural network with some constraints
satisfied exactly [Simic:90a]. This can also be understood by
generalizing the conventional binary neurons to multistate or Potts
variables
[Peterson:89b;90a;93a].
Moscato developed several novel ways of combining simulated annealing
with genetic algorithms [Moscato:89a;89c;89d;89e]
and
showed the power and flexibility of these methods.





Next: An Improved Method
Up: 11 Load Balancing and
Previous: Applications and Extensions
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
 P maintained a significant activity in optimization.
There were several reasons for this, one of which
was, of course, natural curiosity. Another was the importance of load
balancing and data decomposition which is, as discussed previously in
this chapter, ``just'' an optimization problem. Again, we already
mentioned in Section 6.1 our interest in neural
networks as a naturally parallel approach to
artificial intelligence. Section 9.9 and Section 11.1 have
shown how neural networks can be used in a range of optimization
problems. Load balancing has the important (optimization)
characteristic of NP completeness, which implies that it would take an
exponential time to solve completely. Thus, we studied the travelling
salesman problem (TSP) which is well known to be NP-complete and
formally equivalent to other problems with this property. One
important contribution of C
P maintained a significant activity in optimization.
There were several reasons for this, one of which
was, of course, natural curiosity. Another was the importance of load
balancing and data decomposition which is, as discussed previously in
this chapter, ``just'' an optimization problem. Again, we already
mentioned in Section 6.1 our interest in neural
networks as a naturally parallel approach to
artificial intelligence. Section 9.9 and Section 11.1 have
shown how neural networks can be used in a range of optimization
problems. Load balancing has the important (optimization)
characteristic of NP completeness, which implies that it would take an
exponential time to solve completely. Thus, we studied the travelling
salesman problem (TSP) which is well known to be NP-complete and
formally equivalent to other problems with this property. One
important contribution of C P was the work of Simic
[Simic:90a;91a]. [Simic:91a]
P was the work of Simic
[Simic:90a;91a]. [Simic:91a]





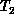 by the solution at the
previous higher temperature
by the solution at the
previous higher temperature 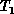 . This annealing can be applied
either statistically [
. This annealing can be applied
either statistically [