




Next: Convectively-Dominated Flows and
Up: 6 Synchronous Applications II
Previous: 6 Synchronous Applications II
Synchronous problems have been defined in Section 3.4 as
having the simplest temporal or computational structure. The problems
are typically defined by a regular grid, as illustrated in
Figure 4.3, and are parallelized by a simple domain
decomposition. A synchronous temporal structure corresponds to each point in the data domain being evolved
with an identical computational algorithm, and we summarize this in the
caricature shown in Figure 6.1. We find several
important synchronous problems in the academic applications, which
formed the core of C P's work. We expect-as shown in
Chapter 19-that the ``real world'' (industry and government)
will show fewer problems of the synchronous class. One hopes that a
fundamental theory will describe phenomena in terms of simple elegant
and uniform laws; these are likely to lead to a synchronous or
computational (temporal) structure. On the other hand, real-world
problems typically involve macroscopic phenomenological models as
opposed to fundamental theories of the microscopic world.
Correspondingly, we find in the real world more loosely synchronous
problems that only exhibit macroscopic temporal synchronization.
P's work. We expect-as shown in
Chapter 19-that the ``real world'' (industry and government)
will show fewer problems of the synchronous class. One hopes that a
fundamental theory will describe phenomena in terms of simple elegant
and uniform laws; these are likely to lead to a synchronous or
computational (temporal) structure. On the other hand, real-world
problems typically involve macroscopic phenomenological models as
opposed to fundamental theories of the microscopic world.
Correspondingly, we find in the real world more loosely synchronous
problems that only exhibit macroscopic temporal synchronization.

Figure 6.1: The Synchronous Problem Class
There is no black-and-white definition of synchronous since, practically,
we allow some violations of the rigorous microscopic synchronization.
This is already seen in Section 4.2's discussion of the
irregularity of Monte Carlo ``accept-reject''
algorithms. A deeper example is irregular geometry problems, such as
the partial differential equations of Chapters 9 and
12 with an irregular mesh. The simplest of these can be
implemented well on SIMD machines as long as each node can access
different addresses. In the High Performance Fortran analysis of
Chapter 13, there is a class of problems lacking the regular
grid of Figure 4.3. They cannot be expressed in terms of
Fortran 90 with arrays of values. However, the simpler irregular
meshes are topologically rectangular-they can be expressed in
Fortran 90 with an array of pointers. The SIMD Maspar
MP-1,2 supports this node-dependent addressing and has termed this an
``autonomous SIMD'' feature. We believe that just as SIMD is not a
precise computer architecture, the synchronous problem class will also
inevitably be somewhat vague, with some problems having architectures
in a grey area between synchronous and loosely synchronous.
The applications described in Chapter 4 were all run on MIMD
machines using the message-passing model of Chapter 5.
Excellent speedups were obtained. Interestingly, even when C P
acquired a SIMD CM-2, which also supported this problem class well, we
found it hard to move onto this machine because of the different
software model-the data parallel languages of
Chapter 13-offered by SIMD machines. The development of High
Performance Fortran, reviewed in Section 13.1, now offers the same
data-parallel programming model on SIMD and MIMD machines for
synchronous problems. Currently, nobody has efficiently ported the
message-passing model to SIMD machines-even with the understanding
that it would only be effective for synchronous problems. It may be
that with the last obvious restriction, the message-passing model could
be implemented on SIMD machines.
P
acquired a SIMD CM-2, which also supported this problem class well, we
found it hard to move onto this machine because of the different
software model-the data parallel languages of
Chapter 13-offered by SIMD machines. The development of High
Performance Fortran, reviewed in Section 13.1, now offers the same
data-parallel programming model on SIMD and MIMD machines for
synchronous problems. Currently, nobody has efficiently ported the
message-passing model to SIMD machines-even with the understanding
that it would only be effective for synchronous problems. It may be
that with the last obvious restriction, the message-passing model could
be implemented on SIMD machines.
This chapter includes a set of neural network
applications. This is an important class of naturally parallel
problems, and represents one approach to answering the question:
``How can one apply massively parallel machines to artificial
intelligence (AI)?''
We were asked this many times at the start of C P, since AI was one of
the foremost fields in computer science at the time. Today, the
initial excitement behind the Japanese fifth-generation project has
abated and AI has transitioned to a routine production technology which
is perhaps more limited than originally believed. Interestingly, the
neural network approach leads to synchronous structure, whereas the
complementary actor or expert system approaches have a very
different asynchronous structure.
The high temperature superconductivity calculations in
Section 6.3 made a major impact on the condensed matter community. Quoting from Nature [Maddox:90a]
P, since AI was one of
the foremost fields in computer science at the time. Today, the
initial excitement behind the Japanese fifth-generation project has
abated and AI has transitioned to a routine production technology which
is perhaps more limited than originally believed. Interestingly, the
neural network approach leads to synchronous structure, whereas the
complementary actor or expert system approaches have a very
different asynchronous structure.
The high temperature superconductivity calculations in
Section 6.3 made a major impact on the condensed matter community. Quoting from Nature [Maddox:90a]
``Yet some progress seems to have been made. Thus Hong-Qiang Ding and
Miloje S. Makivic, from California Institute of Technology, now
describe an exceedingly powerful Monte Carlo
calculation of an antiferromagnetic lattice designed to allow for the
simulation of 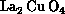 (Phys. Rev. Lett. 64,
1,449; 1990). In this context, a Monte Carlo simulation entails
starting with an arbitrary arrangement of spins on the lattice, and
then changing them in pairs according to rules that allow all spin
states to be reached without violating the overall constraints. The
authors rightly boast of their access to Caltech's parallel computer
system, but they have also devised a new and efficient algorithm for
tracing out the evolution of their system. As is the custom in this
part of the trade, they have worked with square patches of
two-dimensional lattice with as many as 128 lattice spacings to each
side.
(Phys. Rev. Lett. 64,
1,449; 1990). In this context, a Monte Carlo simulation entails
starting with an arbitrary arrangement of spins on the lattice, and
then changing them in pairs according to rules that allow all spin
states to be reached without violating the overall constraints. The
authors rightly boast of their access to Caltech's parallel computer
system, but they have also devised a new and efficient algorithm for
tracing out the evolution of their system. As is the custom in this
part of the trade, they have worked with square patches of
two-dimensional lattice with as many as 128 lattice spacings to each
side.
The outcome is a relationship between correlation length-the
distance over which order, on the average, persists-and
temperature; briefly, the logarithm of the correlation length is
inversely proportional to the temperature. That, apparently,
contradicts other models of the ordering process. In lanthanum copper
oxide, the correlation length agrees well with that measured by
neutron diffraction below  (where there is a phase
transition), provided the interaction energy is chosen appropriately.
For what it is worth, that energy is not very different from estimates
derived from Raman-scattering experiments, which provide a direct
measurement of the energy of interaction by the change of frequency of
the scattered light.''
(where there is a phase
transition), provided the interaction energy is chosen appropriately.
For what it is worth, that energy is not very different from estimates
derived from Raman-scattering experiments, which provide a direct
measurement of the energy of interaction by the change of frequency of
the scattered light.''
The hypercube allowed much larger high- calculations than the
previous state of the art, with conventional machines. Curiously,
with QCD simulations (described in Section 4.3), we were only
able at best to match the size of the Cray calculations of other
groups. This probably reflects different cultures and computational
expectations of the QCD and condensed matter
communities. C
calculations than the
previous state of the art, with conventional machines. Curiously,
with QCD simulations (described in Section 4.3), we were only
able at best to match the size of the Cray calculations of other
groups. This probably reflects different cultures and computational
expectations of the QCD and condensed matter
communities. C P had the advantage of dedicated facilities and
could devote them to the most interesting applications.
P had the advantage of dedicated facilities and
could devote them to the most interesting applications.
Section 6.2 describes an early calculation, which was a
continuation of our collaboration with Sandia on nCUBE
applications. They, of course, followed this with a major internal
activity, including their impressive performance analysis of 1024-node applications
[Gustafson:88a]. There were several other synchronous
applications in C P that we will not describe in this book. Wasson
solved the single-particle Schrödinger equation in a regular grid to
study the ground state of nuclear matter as a
function of temperature and pressure. His approach used the
time-dependent Hartree-Fock method, but was never taken past the stage
of preliminary calculations on the early Mark II machines
[Wasson:87a]. There were also two interesting signal-processing
algorithms. Pollara implemented the Viterbi algorithm
for convolutional decoding of data sent on noisy
communication channels [Pollara:85a], [Pollara:86a]. This
has similarities with the Cooley-Tukey binary FFT
parallelization described in [Fox:88a]. We also looked at
alternatives to this binary FFT in a collaboration with Aloisio from
the Italian Space Agency. The prime number (nonbinary) discrete
Fourier transform produces a more irregular communication pattern than
the binary FFT and, further, the node calculations are less easy to
pipeline than the conventional FFT. Thus, it is hard to achieve the
theoretical advantage of the nonbinary FFT. This often has less
floating-point operations needed for a given analysis whose natural
problem size may not be the power of two demanded by the binary FFT
P that we will not describe in this book. Wasson
solved the single-particle Schrödinger equation in a regular grid to
study the ground state of nuclear matter as a
function of temperature and pressure. His approach used the
time-dependent Hartree-Fock method, but was never taken past the stage
of preliminary calculations on the early Mark II machines
[Wasson:87a]. There were also two interesting signal-processing
algorithms. Pollara implemented the Viterbi algorithm
for convolutional decoding of data sent on noisy
communication channels [Pollara:85a], [Pollara:86a]. This
has similarities with the Cooley-Tukey binary FFT
parallelization described in [Fox:88a]. We also looked at
alternatives to this binary FFT in a collaboration with Aloisio from
the Italian Space Agency. The prime number (nonbinary) discrete
Fourier transform produces a more irregular communication pattern than
the binary FFT and, further, the node calculations are less easy to
pipeline than the conventional FFT. Thus, it is hard to achieve the
theoretical advantage of the nonbinary FFT. This often has less
floating-point operations needed for a given analysis whose natural
problem size may not be the power of two demanded by the binary FFT
[Aloisio:88a;89b;90b;91a;91b]. This parallel discrete FFT was designed
for synthetic aperture radar applications for the analysis of satellite
data [Aloisio:90c;90d].
The applications in Sections 6.7.3, 6.5, and
6.6 use the important multiscale approach to a
variety of vision or image processing
problems. Essentially, all physical problems are usefully considered
at several different length scales, and we will come back to this in
Chapters 9 and 12 when we study partial differential
equations (multigrid) and practice dynamics (fast multipole).





Next: Convectively-Dominated Flows and
Up: 6 Synchronous Applications II
Previous: 6 Synchronous Applications II
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
 P's work. We expect-as shown in
Chapter 19-that the ``real world'' (industry and government)
will show fewer problems of the synchronous class. One hopes that a
fundamental theory will describe phenomena in terms of simple elegant
and uniform laws; these are likely to lead to a synchronous or
computational (temporal) structure. On the other hand, real-world
problems typically involve macroscopic phenomenological models as
opposed to fundamental theories of the microscopic world.
Correspondingly, we find in the real world more loosely synchronous
problems that only exhibit macroscopic temporal synchronization.
P's work. We expect-as shown in
Chapter 19-that the ``real world'' (industry and government)
will show fewer problems of the synchronous class. One hopes that a
fundamental theory will describe phenomena in terms of simple elegant
and uniform laws; these are likely to lead to a synchronous or
computational (temporal) structure. On the other hand, real-world
problems typically involve macroscopic phenomenological models as
opposed to fundamental theories of the microscopic world.
Correspondingly, we find in the real world more loosely synchronous
problems that only exhibit macroscopic temporal synchronization.






 P
acquired a SIMD CM-2, which also supported this problem class well, we
found it hard to move onto this machine because of the different
software model-the data parallel languages of
Chapter
P
acquired a SIMD CM-2, which also supported this problem class well, we
found it hard to move onto this machine because of the different
software model-the data parallel languages of
Chapter  P, since AI was one of
the foremost fields in computer science at the time. Today, the
initial excitement behind the Japanese fifth-generation project has
abated and AI has transitioned to a routine production technology which
is perhaps more limited than originally believed. Interestingly, the
neural network approach leads to synchronous structure, whereas the
complementary actor or expert system approaches have a very
different asynchronous structure.
The high temperature superconductivity
P, since AI was one of
the foremost fields in computer science at the time. Today, the
initial excitement behind the Japanese fifth-generation project has
abated and AI has transitioned to a routine production technology which
is perhaps more limited than originally believed. Interestingly, the
neural network approach leads to synchronous structure, whereas the
complementary actor or expert system approaches have a very
different asynchronous structure.
The high temperature superconductivity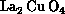 (Phys. Rev. Lett. 64,
1,449; 1990). In this context, a Monte Carlo simulation entails
starting with an arbitrary arrangement of spins on the lattice, and
then changing them in pairs according to rules that allow all spin
states to be reached without violating the overall constraints. The
authors rightly boast of their access to Caltech's parallel computer
system, but they have also devised a new and efficient algorithm for
tracing out the evolution of their system. As is the custom in this
part of the trade, they have worked with square patches of
two-dimensional lattice with as many as 128 lattice spacings to each
side.
(Phys. Rev. Lett. 64,
1,449; 1990). In this context, a Monte Carlo simulation entails
starting with an arbitrary arrangement of spins on the lattice, and
then changing them in pairs according to rules that allow all spin
states to be reached without violating the overall constraints. The
authors rightly boast of their access to Caltech's parallel computer
system, but they have also devised a new and efficient algorithm for
tracing out the evolution of their system. As is the custom in this
part of the trade, they have worked with square patches of
two-dimensional lattice with as many as 128 lattice spacings to each
side.
 (where there is a phase
transition), provided the interaction energy is chosen appropriately.
For what it is worth, that energy is not very different from estimates
derived from Raman-scattering experiments, which provide a direct
measurement of the energy of interaction by the change of frequency of
the scattered light.''
(where there is a phase
transition), provided the interaction energy is chosen appropriately.
For what it is worth, that energy is not very different from estimates
derived from Raman-scattering experiments, which provide a direct
measurement of the energy of interaction by the change of frequency of
the scattered light.''
 calculations than the
previous state of the art, with conventional machines. Curiously,
with QCD simulations (described in Section
calculations than the
previous state of the art, with conventional machines. Curiously,
with QCD simulations (described in Section  P had the advantage of dedicated facilities and
could devote them to the most interesting applications.
P had the advantage of dedicated facilities and
could devote them to the most interesting applications.
 P that we will not describe in this book. Wasson
solved the single-particle Schrödinger equation in a regular grid to
study the ground state of nuclear matter
P that we will not describe in this book. Wasson
solved the single-particle Schrödinger equation in a regular grid to
study the ground state of nuclear matter