




Next: 6.6.3 The Multiscale Technique
Up: 6.6 Character Recognition by
Previous: 6.6.1 MLP in General
To do character recognition using an MLP,
we assume the input layer of the network to be a set of image pixels,
which can take on analogue (or grey scale) values between 0 and 1. The
two-dimensional set of pixels is mapped onto the set of input neurons
in a fairly arbitrary way: For an 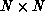 image, the top row of
N pixels is associated with the first N neurons, the next row of
N pixels is associated with the next N neurons, and so forth. At
the start of the training process, the network has no knowledge of the
underlying two-dimensional structure of the problem (that is, if a
pixel is on, nearby pixels in the two-dimensional space are also likely
to be on). The network discovers the two-dimensional nature of the
problem during the learning process.
image, the top row of
N pixels is associated with the first N neurons, the next row of
N pixels is associated with the next N neurons, and so forth. At
the start of the training process, the network has no knowledge of the
underlying two-dimensional structure of the problem (that is, if a
pixel is on, nearby pixels in the two-dimensional space are also likely
to be on). The network discovers the two-dimensional nature of the
problem during the learning process.
We taught our networks the alphabet of 26 upper-case Roman characters. To
encourage generalization, we show the net many different hand-drawn versions
of each character. The 320-image training set is shown in
Figure 6.32. These images were hand-drawn using a mouse attached
to a SUN workstation. The output is encoded in a very sparse way. There are
only 26 outputs we want the net to give, so we use 26 output neurons and map
the output pattern: first neuron on, rest off, to the character ``A;''
second neuron on, rest off, to ``B;'' and so on. Such an encoding
scheme works well here, but is clearly unworkable for mappings with large
output sets such as Chinese characters or Kanji. In such cases, one would
prefer a more compact output encoding, with possibly an additional layer of
hidden units to produce the more complex outputs.

Figure 6.32: The Training Set of 320 Handwritten Characters, Digitized on a
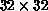 Grid
Grid
As mentioned earlier, we do not feed images directly into the network.
Instead, simple, automatic preprocessing is done which dilates the image to
a standard size and then translates it to the center of the pixel space.
This greatly enhances the performance of the system-it means that one can
draw a character in the upper left-hand corner of the pixel space and the
system easily recognizes it. If we did not have the preprocessing, the
network would be forced to solve the much larger problem of character
recognition of all possible sizes and locations in the pixel space. Two
other worthwhile preprocessors are rotations (rotate to a standard
orientation) and intensity normalization (set linewidths to some standard
value). We do not have these in our current implementation.
The MLP is used only for the part of the algorithm where one matches to
templates. Given any fixed set of exemplars, a neural network will usually
learn this set perfectly, but the performance under generalization can be
very poor. In fact, the more weights there are, the faster the learning (in
the sense of number of iterations, not of CPU time), and the
worse the ability to generalize. This was in part realized in
[Gullichsen:87a], where the input grid was 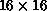 . If one has a
very fine mesh at the input level, so that a great amount of detail can be
seen in the image, one runs the risk of having terrible generalization
properties because the network will tend to focus upon tiny features of the
image, ones which humans would consider irrelevant.
. If one has a
very fine mesh at the input level, so that a great amount of detail can be
seen in the image, one runs the risk of having terrible generalization
properties because the network will tend to focus upon tiny features of the
image, ones which humans would consider irrelevant.
We will show one approach to overcoming this problem. We desire the
potential power of the large, high-resolution net, but with the stable
generalization properties of small, coarse nets. Though not so important for
upper-case Roman characters, where a rather coarse grid does well enough (as
we will see), a fine mesh is necessary for other problems such as recognition
of Kanji characters or handwriting. A possible ``fix,'' similar to what was
done for the problem of clump counting [Denker:87a], is to
hard wire the first layer of weights to be local in space, with a
neighborhood growing with the mesh fineness. This reduces the number of
weights, thus postponing the deterioration of the generalization. However,
for an MLP with a single hidden layer, this approach will prevent the
detection of many nonlocal correlations in the images, and in effect this
fix is like removing the first layer of weights.





Next: 6.6.3 The Multiscale Technique
Up: 6.6 Character Recognition by
Previous: 6.6.1 MLP in General
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
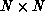 image, the top row of
N pixels is associated with the first N neurons, the next row of
N pixels is associated with the next N neurons, and so forth. At
the start of the training process, the network has no knowledge of the
underlying two-dimensional structure of the problem (that is, if a
pixel is on, nearby pixels in the two-dimensional space are also likely
to be on). The network discovers the two-dimensional nature of the
problem during the learning process.
image, the top row of
N pixels is associated with the first N neurons, the next row of
N pixels is associated with the next N neurons, and so forth. At
the start of the training process, the network has no knowledge of the
underlying two-dimensional structure of the problem (that is, if a
pixel is on, nearby pixels in the two-dimensional space are also likely
to be on). The network discovers the two-dimensional nature of the
problem during the learning process.






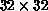 Grid
Grid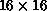 . If one has a
very fine mesh at the input level, so that a great amount of detail can be
seen in the image, one runs the risk of having terrible generalization
properties because the network will tend to focus upon tiny features of the
image, ones which humans would consider irrelevant.
. If one has a
very fine mesh at the input level, so that a great amount of detail can be
seen in the image, one runs the risk of having terrible generalization
properties because the network will tend to focus upon tiny features of the
image, ones which humans would consider irrelevant.