 in the classical model, down to
in the classical model, down to 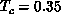 in the quantum
spin-1/2 case, although they are not strong enough to push it down to
0. They also reduced the constant
in the quantum
spin-1/2 case, although they are not strong enough to push it down to
0. They also reduced the constant 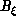 from 1.67 in the
classical case to 1.18 in the spin-1/2 case.
from 1.67 in the
classical case to 1.18 in the spin-1/2 case.





Quantum fluctuations are capable of pushing the transition point from
 in the classical model, down to
in the classical model, down to 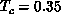 in the quantum
spin-1/2 case, although they are not strong enough to push it down to
0. They also reduced the constant
in the quantum
spin-1/2 case, although they are not strong enough to push it down to
0. They also reduced the constant 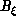 from 1.67 in the
classical case to 1.18 in the spin-1/2 case.
from 1.67 in the
classical case to 1.18 in the spin-1/2 case.
The critical behavior in the quantum case is of the KT-type, as in the
classical case. This is a little surprising, considering the
differences regarding the spin space. In the classical case, the spins
are confined to the X-Y plane (thus the model is conventionally
called a ``planar rotator'' model). This is important for the
topological order in KT theory. The quantum spins are not restricted
to the X-Y plane, due to the presence of 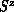 for the commutator
relation. The KT behavior found in the quantum case indicates that the
extra dimension in the spin space (which does not appear in the
Hamiltonian) is actually unimportant. These correlations are very weak
and short-ranged. The out-of-plane susceptibility remains a small
quantity in the whole temperature range.
for the commutator
relation. The KT behavior found in the quantum case indicates that the
extra dimension in the spin space (which does not appear in the
Hamiltonian) is actually unimportant. These correlations are very weak
and short-ranged. The out-of-plane susceptibility remains a small
quantity in the whole temperature range.
These results for the XY model, together with those on the quantum
Heisenberg model, strongly suggest that although quantum fluctuations
at finite T can change the quantitative behavior of these
nonfrustrated spin systems with continuous symmetries, the
qualitative picture of the classical system persists. This could be
understood following universality arguments that, near the critical
point, the dominant behavior of the system is determined by long
wavelength fluctuations which are characterized by symmetries and
dimensionality. The quantum effects only change the short-range
fluctuations which, after integrated out, only enter as renormalization
of the physical parameters, such as 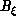 .
.
Our data also show that, for the XY model, the critical exponents are
spin-S independent, in agreement with universality. More specifically,
 in Equation 6.18 could, in principle, differ from its
classical value 1/2. Our data are sufficient to detect any systematic
deviation from this value. For this purpose, we plotted
in Equation 6.18 could, in principle, differ from its
classical value 1/2. Our data are sufficient to detect any systematic
deviation from this value. For this purpose, we plotted 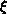 in
Figure 6.18(b), using
in
Figure 6.18(b), using 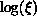 versus
versus 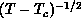 . As
expected, data points all fall well on a straight line (except the point at
. As
expected, data points all fall well on a straight line (except the point at
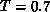 where the critical region presumably ends). A systematic deviation
from
where the critical region presumably ends). A systematic deviation
from 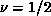 would lead to a slightly curved line instead of a straight
line. In addition, the exponent,
would lead to a slightly curved line instead of a straight
line. In addition, the exponent, 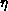 at
at  , seems to be consistent
with the value for the classical system.
, seems to be consistent
with the value for the classical system.
Our simulations reveal a rich structure, as shown in the phase diagram
(Figure 6.21) for these 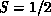 quantum spins. The
antiferromagnetic ordered region and the topological ordered region are
especially relevant to the high-
quantum spins. The
antiferromagnetic ordered region and the topological ordered region are
especially relevant to the high- materials.
materials.
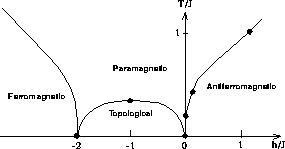
Figure: Phase Diagram for the Spin-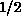 Quantum System Shown in
Equation 6.12. The solid points are from quantum Monte
Carlo simulations. For large
Quantum System Shown in
Equation 6.12. The solid points are from quantum Monte
Carlo simulations. For large  , the system is practically
an Ising system. Near h=0 or h=-2, the logarithmic relation,
Equation 6.16 holds.
, the system is practically
an Ising system. Near h=0 or h=-2, the logarithmic relation,
Equation 6.16 holds.
Finally, we point out the connection between the quantum XY system
and the general two-dimensional quantum system with continuous
symmetry. Through the above-mentioned Matsubara-Matsuda
transformations, our result implies the existence of the
Kosterlitz-Thouless condensation in two-dimensional quantum systems.
The symmetry in the XY model now becomes  , a continuous phase symmetry. This quantum KT
condensation may have important implications on the mechanism of the
recently discovered high-temperature superconducting transitions.
, a continuous phase symmetry. This quantum KT
condensation may have important implications on the mechanism of the
recently discovered high-temperature superconducting transitions.




