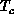It is well known now that the two-dimensional (2D) classical (planar) XY
model undergoes Kosterlitz-Thouless (KT)
[Kosterlitz:73a] transition at
[Gupta:88a], characterized by exponentially divergent
correlation length and in-plane susceptibility. The transition, due to the
unbinding of vortex-antivortex pairs, is weak; the specific heat has a finite
peak above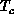 
.
Does the two-dimensional quantum XY model go
through a phase transition? If so, what type of transition? This is a
longstanding problem in statistical physics. The answers are relevant
to a wide class of two-dimensional problems such as magnetic
insulators, superfluidity, melting, and possibly to the recently
discovered high-
superconducting transition. Physics in two
dimensions is characterized by large fluctuations. Changing from the
classical model to the quantum model, additional quantum fluctuations
(which are particularly strong in the case of spin-1/2) may alter the
physics significantly. A direct consequence is that the already weak
KT transition could be washed out completely.