Eigenvalue Problems

 

ScaLAPACK includes block algorithms for solving symmetric  and nonsymmetric eigenvalue problems as well as for computing the singular value decomposition.

The first step in solving many types of eigenvalue problems is to reduce the original matrix to a ``condensed form'' by orthogonal transformations.     In the reduction to condensed forms, the unblocked algorithms all use elementary Householder matrices and have good vector performance. Block forms of these algorithms have been developed [28], but all require additional operations, and a significant proportion of the work must still be performed by the Level 2 PBLAS. Thus, there is less possibility of compensating for the extra operations.

The algorithms concerned are listed below:

• Reduction of a symmetric matrix to tridiagonal form  to solve a symmetric eigenvalue problem: ScaLAPACK routine PSSYTRD /PDSYTRD  applies a symmetric block update of the form
  
  using the Level 3 PBLAS routine PSSYR2K /PDSYR2K ; Level 3 PBLAS account for at most half the work.
• Reduction of a rectangular matrix to bidiagonal form  to compute a singular value decomposition: ScaLAPACK routine PSGEBRD  /PDGEBRD  applies a block update of the form
  
  using two calls to the Level 3 PBLAS routine PSGEMM/PDGEMM; Level 3 PBLAS account for at most half the work.
• Reduction of a nonsymmetric matrix to Hessenberg form   to solve a nonsymmetric eigenvalue problem: ScaLAPACK routine PSGEHRD /PDGEHRD  applies a block update of the form
  
  Level 3 PBLAS account for at most three-quarters of the work.

Extra work must be performed to compute the N-by-K matrices X and Y that are required for the block updates (K is the block size), and extra workspace is needed to store them.

Following the reduction of a dense symmetric matrix to tridiagonal form T, one must compute the eigenvalues and (optionally) eigenvectors of T. The current version of ScaLAPACK includes two different routines PSSYEVX /PDSYEVX  and PSSYEV /PDSYEV  for solving symmetric eigenproblems. PSSYEVX/PDSYEVX uses bisection and inverse iteration. PSSYEV/PDSYEV uses the QR algorithm. Table 5.12  and Table 5.13  show the execution time in seconds of the routines PSSYEVX/PDSYEVX and PSSYEV /PDSYEV , respectively, for computing the eigenvalues and eigenvectors of symmetric matrices of order N. The performance of PSSYEVX /PDSYEVX  deteriorates in the face of large clusters of eigenvalues. ScaLAPACK uses a nonscalable definition of clusters (because we chose to remain consistent with LAPACK). Hence, matrices larger than N=1000 tend to have at least one very large cluster (see section 5.3.6). This needs further study. More detailed information concerning the performance of these routines may be found in [40]. Table 5.14  shows the execution time in seconds of the routines PSGESVD /PDGESVD  for computing the singular values and the corresponding right and left singular vectors of a general matrix of order N.

  
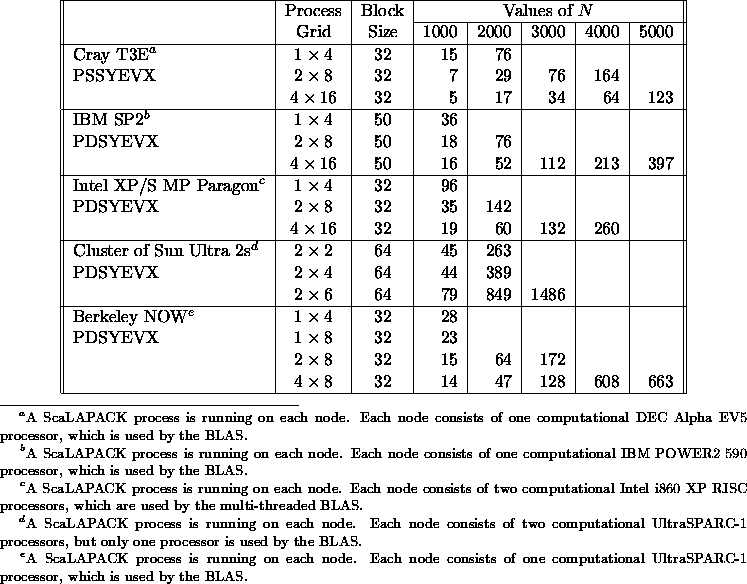
Table 5.12: Execution time in seconds of PSSYEVX/PDSYEVX for square matrices of order N

For computing the eigenvalues and eigenvectors of a Hessenberg matrix--or rather, for computing its Schur factorization-- two flavors of block algorithms have been developed. The first algorithm implemented in the routine PSLAHQR /PDLAHQR  results from the parallelization of the QR algorithm. The key idea is to generate many shifts at once rather than two at a time, thereby allowing all bulges to carry out up-to-date shifts. The second algorithm that is currently implemented as a prototype code  is based on the computation of the matrix sign function [14, 13, 12]. In this section, however, only performance results of the first approach are reported.

  
Table 5.13: Execution time in seconds of PSSYEV/PDSYEV for square matrices of order N

  
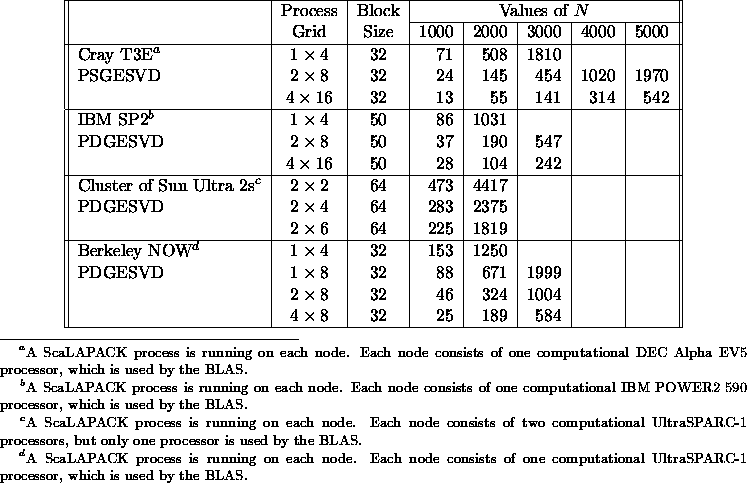
Table 5.14: Execution time in seconds of PSGESVD/PDGESVD for square matrices of order N

Table 5.15  summarizes performance results obtained for the ScaLAPACK routine PDLAHQR doing a full Schur decomposition of an order N upper Hessenberg matrix. The supercomputers the table gives timings for are the Intel XP/S MP Paragon supercomputer and technology from the Intel ASCI Option Red Supercomputer. For both machines, we assume only one CPU is being used for computation on this code. The Schur decomposition is based on iteratively applying orthogonal similarity transformations on a Hessenberg matrix H such as

until T becomes pseudo-upper triangular (i.e., in the real case, having one by one or two by two subdiagonal blocks.) The serial performance (assuming roughly 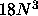flops) of the LAPACK routine DLAHQR for computing a complex Schur decomposition is around 8.5 Mflops on the Intel MP Paragon supercomputer. The enhanced performance shown in Table 5.15 is slightly faster, a bit above 9 Mflops, and ends up peaking around 10 Mflops because of the block application of Householder transforms found in the ScaLAPACK serial auxiliary routine DLAREF. For the technology behind the Intel ASCI Option Red Supercomputer, it peaks at several times the speed of the Paragon, and has a slightly faster drop off in efficiency. For further details and timings, please see [79].

  
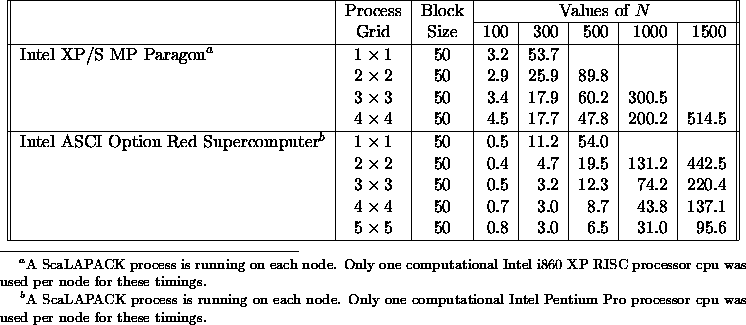
Table 5.15: Execution time in seconds of PDLAHQR for square matrices of order N

A more detailed performance analysis of the eigensolvers included in the ScaLAPACK software library can be found in [48, 79]. Finally, we note that research into parallel algorithms for symmetric and nonsymmetric eigenproblems continues [11, 86, 45], and future versions of ScaLAPACK will be updated to contain the best algorithms available.