Table 5.11
summarizes performance results obtained for the ScaLAPACK routine
PSGELS /PDGELS that
solves full-rank linear least squares problems. Solving such problems
of the form 
, where x and b
are vectors and A is a rectangular matrix having full rank is
traditionally achieved via the computation of the QR factorization
of the matrix A. In ScaLAPACK, the QR factorization
is based on the use of elementary Householder
matrices of the general form
where v is a column vector and 
is a scalar. This leads
to an algorithm with excellent vector performance, especially
if coded to use Level 2 PBLAS.
The key to developing a distributed block form of this algorithm
is to represent a product of K elementary Householder
matrices of order N as a block form of a Householder matrix.
This can be done in various ways. ScaLAPACK uses the form
[108]
where V is an N-by-K matrix whose columns are the
individual vectors 
associated with
the Householder matrices 
and T
is an upper triangular matrix of order K. Extra work is
required to compute the elements of T, but this is compensated
for by the greater speed of applying the block form.
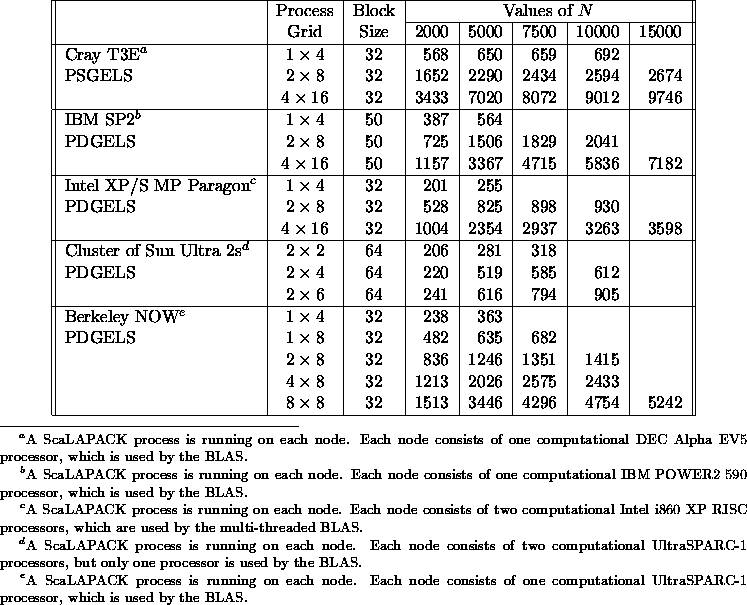
Table 5.11: Speed in Mflop/s of PSGELS/PDGELS for square matrices of
order N