References

1

M. ABOELAZE, N. CHRISOCHOIDES, AND E. HOUSTIS, The Parallelization of Level 2 and 3 BLAS Operations on Distributed Memory Machines, Tech. Rep. CSD-TR-91-007, Purdue University, West Lafayette, IN, 1991.

2

R. AGARWAL, F. GUSTAVSON, AND M. ZUBAIR, Improving Performance of Linear Algebra Algorithms for Dense Matrices Using Algorithmic Prefetching, IBM J. Res. Dev., 38 (1994), pp. 265-275.

3

E. ANDERSON, Z. BAI, C. BISCHOF, J. DEMMEL, J. DONGARRA, J. DU CROZ, A. GREENBAUM, S. HAMMARLING, A. MCKENNEY, S. OSTROUCHOV, AND D. SORENSEN, LAPACK Users' Guide, Society for Industrial and Applied Mathematics, Philadelphia, PA, second ed., 1995.

4

E. ANDERSON, Z. BAI, C. BISCHOF, J. DEMMEL, J. DONGARRA, J. DU CROZ, A. GREENBAUM, S. HAMMARLING, A. MCKENNEY, AND D. SORENSEN, LAPACK: A portable linear algebra library for high-performance computers, Computer Science Dept. Technical Report CS-90-105, University of Tennessee, Knoxville, TN, May 1990. (Also LAPACK Working Note #20).

5

E. ANDERSON, Z. BAI, AND J. DONGARRA, Generalized QR factorization and its applications, Linear Algebra and Its Applications, 162-164 (1992), pp. 243-273. (Also LAPACK Working Note #31).

6

I. ANGUS, G. FOX, J. KIM, AND D. WALKER, Solving Problems on Concurrent Processors: Software for Concurrent Processors, vol. 2, Prentice Hall, Englewood Cliffs, N.J, 1990.

7

ANSI/IEEE, IEEE Standard for Binary Floating Point Arithmetic, New York, Std 754-1985 ed., 1985.

8

height 2pt depth -1.6pt width 23pt, IEEE Standard for Radix Independent Floating Point Arithmetic, New York, Std 854-1987 ed., 1987.

9

M. ARIOLI, J. W. DEMMEL, AND I. S. DUFF, Solving sparse linear systems with sparse backward error, SIAM J. Matrix Anal. Appl., 10 (1989), pp. 165-190.

10

C. ASHCRAFT, The Distributed Solution of Linear Systems Using the Torus-wrap Data mapping, Tech. Rep. ECA-TR-147, Boeing Computer Services, Seattle, WA, 1990.

11

Z. BAI AND J. DEMMEL, Design of a parallel nonsymmetric eigenroutine toolbox, Part I, in Proceedings of the Sixth SIAM Conference on Parallel Processing for Scientific Computing, SIAM, 1993, pp. 391-398.

12

Z. BAI AND J. DEMMEL, Using the matrix sign function to compute invariant subspaces, SIAM J. Matrix Anal. Appl, x (1997), p. xxx. to appear.

13

Z. BAI, J. DEMMEL, J. DONGARRA, A. PETITET, H. ROBINSON, AND K. STANLEY, The spectral decomposition of nonsymmetric matrices on distributed memory computers, Computer Science Dept. Technical Report CS-95-273, University of Tennessee, Knoxville, TN, 1995. (Also LAPACK Working Note No. 91), To appear in SIAM J. Sci. Stat. Comput.

14

Z. BAI AND J. W. DEMMEL, Design of a parallel nonsymmetric eigenroutine toolbox, Part I, in Proceedings of the Sixth SIAM Conference on Parallel Processing for Scientific Computing, R. F. et al. Sincovec, ed., Philadelphia, PA, 1993, Society for Industrial and Applied Mathematics, pp. 391-398. Long version available as Computer Science Report CSD-92-718, University of California, Berkeley, 1992.

15

J. BARLOW AND J. DEMMEL, Computing accurate eigensystems of scaled diagonally dominant matrices, SIAM J. Num. Anal., 27 (1990), pp. 762-791. (Also LAPACK Working Note #7).

16

J. BILMES, K. ASANOVIC, J. DEMMEL, D. LAM, AND C. CHIN, Optimizing matrix multiply using PHiPAC: A portable, high-performance, ANSI C coding methodology, Computer Science Dept. Technical Report CS-96-326, University of Tennessee, Knoxville, TN, 1996. (Also LAPACK Working Note #111).

17

R. H. BISSELING AND J. G. G. VAN DE VORST, Parallel LU decomposition on a transputer network, in Lecture Notes in Computer Science, Number 384, G. A. van Zee and J. G. G. van de Vorst, eds., Springer-Verlag, 1989, pp. 61-77.

18

L. S. BLACKFORD, J. CHOI, A. CLEARY, J. DEMMEL, I. DHILLON, J. J. DONGARRA, S. HAMMARLING, G. HENRY, A. PETITET, K. STANLEY, D. W. WALKER, AND R. C. WHALEY, ScaLAPACK: A portable linear algebra library for distributed memory computers - design issues and performance, in Proceedings of Supercomputing '96, Sponsored by ACM SIGARCH and IEEE Computer Society, 1996. (ACM Order Number: 415962, IEEE Computer Society Press Order Number: RS00126. http://www.supercomp.org/sc96/proceedings/).

19

L. S. BLACKFORD, A. CLEARY, J. DEMMEL, I. DHILLON, J. DONGARRA, S. HAMMARLING, A. PETITET, H. REN, K. STANLEY, AND R. C. WHALEY, Practical experience in the dangers of heterogeneous computing, Computer Science Dept. Technical Report CS-96-330, University of Tennessee, Knoxville, TN, July 1996. (Also LAPACK Working Note #112), to appear ACM Trans. Math. Softw., 1997.

20

R. BRENT, The LINPACK Benchmark on the AP 1000, in Frontiers, 1992, McLean, VA, 1992, pp. 128-135.

21

R. BRENT AND P. STRAZDINS, Implementation of BLAS Level 3 and LINPACK Benchmark on the AP1000, Fujitsu Scientific and Technical Journal, 5 (1993), pp. 61-70.

22

S. BROWNE, J. DONGARRA, S. GREEN, E. GROSSE, K. MOORE, T. ROWAN, AND R. WADE, Netlib services and resources (rev. 1), Computer Science Dept. Technical Report CS-94-222, University of Tennessee, Knoxville, TN, 1994.

23

S. BROWNE, J. DONGARRA, E. GROSSE, AND T. ROWAN, The netlib mathematical software repository, D-Lib Magazine (www.dlib.org), (1995).

24

J. CHOI, J. DEMMEL, I. DHILLON, J. DONGARRA, S. OSTROUCHOV, A. PETITET, K. STANLEY, D. WALKER, AND R. C. WHALEY, Installation guide for ScaLAPACK, Computer Science Dept. Technical Report CS-95-280, University of Tennessee, Knoxville, TN, March 1995. (Also LAPACK Working Note #93).

25

height 2pt depth -1.6pt width 23pt, ScaLAPACK: A portable linear algebra library for distributed memory computers - design issues and performance, Computer Science Dept. Technical Report CS-95-283, University of Tennessee, Knoxville, TN, March 1995. (Also LAPACK Working Note #95).

26

J. CHOI, J. DONGARRA, S. OSTROUCHOV, A. PETITET, D. WALKER, AND R. C. WHALEY, A proposal for a set of parallel basic linear algebra subprograms, Computer Science Dept. Technical Report CS-95-292, University of Tennessee, Knoxville, TN, May 1995. (Also LAPACK Working Note #100).

27

J. CHOI, J. DONGARRA, R. POZO, AND D. WALKER, ScaLAPACK: A scalable linear algebra library for distributed memory concurrent computers, in Proceedings of the Fourth Symposium on the Frontiers of Massively Parallel Computation, McLean, Virginia, 1992, IEEE Computer Society Press, pp. 120-127. (Also LAPACK Working Note #55).

28

J. CHOI, J. DONGARRA, AND D. WALKER, The design of a parallel dense linear algebra software library: Reduction to Hessenberg, tridiagonal and bidiagonal form, Numerical Algorithms, 10 (1995), pp. 379-399. (Also LAPACK Working Note #92).

29

J. CHOI, J. DONGARRA, AND D. WALKER, PB-BLAS: A Set of Parallel Block Basic Linear Algebra Subroutines, Concurrency: Practice and Experience, 8 (1996), pp. 517-535.

30

A. CHTCHELKANOVA, J. GUNNELS, G. MORROW, J. OVERFELT, AND R. VAN DE GEIJN, Parallel Implementation of BLAS: General Techniques for Level 3 BLAS, Tech. Rep. TR95-49, Department of Computer Sciences, UT-Austin, 1995. Submitted to Concurrency: Practice and Experience.

31

E. CHU AND A. GEORGE, QR Factorization of a Dense Matrix on a Hypercube Multiprocessor, SIAM Journal on Scientific and Statistical Computing, 11 (1990), pp. 990-1028.

32

A. CLEARY AND J. DONGARRA, Implementation in scalapack of divide-and-conquer algorithms for banded and tridiagonal linear systems, Computer Science Dept. Technical Report CS-97-358, University of Tennessee, Knoxville, TN, April 1997. (Also LAPACK Working Note #125).

33

M. COSNARD, Y. ROBERT, P. QUINTON, AND M. TCHUENTE, eds., Parallel Algorithms and Architectures, North-Holland, 1986.

34

D. E. CULLER, A. ARPACI-DUSSEAU, R. ARPACI-DUSSEAU, B. CHUN, S. LUMETTA, A. MAINWARING, R. MARTIN, C. YOSHIKAWA, AND F. WONG, Parallel computing on the Berkeley NOW. To appear in JSPP'97 (9th Joint Symposium on Parallel Processing), Kobe, Japan, 1997.

35

M. DAYDE, I. DUFF, AND A. PETITET, A Parallel Block Implementation of Level 3 BLAS for MIMD Vector Processors, ACM Trans. Math. Softw., 20 (1994), pp. 178-193.

36

B. DE MOOR AND P. VAN DOOREN, Generalization of the singular value and QR decompositions, SIAM J. Matrix Anal. Appl., 13 (1992), pp. 993-1014.

37

J. DEMMEL, Underflow and the reliability of numerical software, SIAM J. Sci. Stat. Comput., 5 (1984), pp. 887-919.

38

height 2pt depth -1.6pt width 23pt, Applied Numerical Linear Algebra, SIAM, 1996. to appear.

39

J. DEMMEL, S. EISENSTAT, J. GILBERT, X. LI, AND J. W. H. LIU, A supernodal approach to sparse partial pivoting, Technical Report UCB//CSD-95-883, UC Berkeley Computer Science Division, September 1995. to appear in SIAM J. Mat. Anal. Appl.

40

J. DEMMEL AND K. STANLEY, The performance of finding eigenvalues and eigenvectors of dense symmetric matrices on distributed memory computers, Computer Science Dept. Technical Report CS-94-254, University of Tennessee, Knoxville, TN, September 1994. (Also LAPACK Working Note #86).

41

J. W. DEMMEL, J. R. GILBERT, AND X. S. LI, An asynchronous parallel supernodal algorithm for sparse Gaussian elimination, February 1997. Submitted to SIAM J. Matrix Anal. Appl., special issue on Sparse and Structured Matrix Computations and Their Applications (Also LAPACK Working Note 124).

42

J. W. DEMMEL AND X. LI, Faster numerical algorithms via exception handling, IEEE Trans. Comp., 43 (1994), pp. 983-992. (Also LAPACK Working Note #59).

43

I. S. DHILLON, Current inverse iteration software can fail, (1997). Submitted for publication.

44

height 2pt depth -1.6pt width 23pt, A Stable 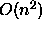Algorithm for the Symmetric Tridiagonal Eigenproblem, PhD thesis, University of California, Berkeley, CA, May 1997.

45

I. S. DHILLON AND B. PARLETT, Orthogonal eigenvectors without Gram-Schmidt, (1997). draft.

46

J. DONGARRA AND T. DUNIGAN, Message-passing performance of various computers, Tech. Rep. ORNL/TM-13006, Oak Ridge National Laboratory, Oak Ridge, TN, 1996. Submitted and accepted to Concurrency: Practice and Experience.

47

J. DONGARRA, S. HAMMARLING, AND D. WALKER, Key Concepts for Parallel Out-Of-Core LU Factorization, Society for Industrial and Applied Mathematics, Philadelphia, PA, 1996. (Also LAPACK Working Note #110).

48

J. DONGARRA, G. HENRY, AND D. WATKINS, A distributed memory implementation of the nonsymmetric QR algorithm, in Proceedings of the Eighth SIAM Conference on Parallel Processing for Scientific Computing, Philadelphia, PA, 1997, Society for Industrial and Applied Mathematics.

49

J. DONGARRA, C. RANDRIAMARO, L. PRYLLI, AND B. TOURANCHEAU, Array redistribution in ScaLAPACK using PVM, in EuroPVM users' group, Hermes, 1995.

50

J. DONGARRA AND R. VAN DE GEIJN, Two dimensional basic linear algebra communication subprograms, Computer Science Dept. Technical Report CS-91-138, University of Tennessee, Knoxville, TN, 1991. (Also LAPACK Working Note #37).

51

J. DONGARRA, R. VAN DE GEIJN, AND D. WALKER, Scalability issues in the design of a library for dense linear algebra, Journal of Parallel and Distributed Computing, 22 (1994), pp. 523-537. (Also LAPACK Working Note #43).

52

J. DONGARRA, R. VAN DE GEIJN, AND R. C. WHALEY, Two dimensional basic linear algebra communication subprograms, in Environments and Tools for Parallel Scientific Computing, Advances in Parallel Computing, J. Dongarra and B. Tourancheau, eds., vol. 6, Elsevier Science Publishers B.V., 1993, pp. 31-40.

53

J. DONGARRA AND D. WALKER, Software libraries for linear algebra computations on high performance computers, SIAM Review, 37 (1995), pp. 151-180.

54

J. DONGARRA AND R. C. WHALEY, A user's guide to the BLACS v1.1, Computer Science Dept. Technical Report CS-95-281, University of Tennessee, Knoxville, TN, 1995. (Also LAPACK Working Note #94).

55

J. J. DONGARRA AND E. F. D'AZEVEDO, The design and implementation of the parallel out-of-core ScaLAPACK LU, QR, and Cholesky factorization routines, Department of Computer Science Technical Report CS-97-347, University of Tennessee, Knoxville, TN, 1997. (Also LAPACK Working Note 118).

56

J. J. DONGARRA, J. DU CROZ, I. S. DUFF, AND S. HAMMARLING, Algorithm 679: A set of Level 3 Basic Linear Algebra Subprograms, ACM Trans. Math. Soft., 16 (1990), pp. 18-28.

57

height 2pt depth -1.6pt width 23pt, A set of Level 3 Basic Linear Algebra Subprograms, ACM Trans. Math. Soft., 16 (1990), pp. 1-17.

58

J. J. DONGARRA, J. DU CROZ, S. HAMMARLING, AND R. J. HANSON, Algorithm 656: An extended set of FORTRAN Basic Linear Algebra Subroutines, ACM Trans. Math. Soft., 14 (1988), pp. 18-32.

59

height 2pt depth -1.6pt width 23pt, An extended set of FORTRAN basic linear algebra subroutines, ACM Trans. Math. Soft., 14 (1988), pp. 1-17.

60

J. J. DONGARRA AND E. GROSSE, Distribution of mathematical software via electronic mail, Communications of the ACM, 30 (1987), pp. 403-407.

61

J. J. DONGARRA, R. VAN DE GEIJN, AND D. W. WALKER, A look at scalable dense linear algebra libraries, in Proceedings of the Scalable High-Performance Computing Conference, IEEE, ed., IEEE Publishers, 1992, pp. 372-379.

62

J. DU CROZ AND N. J. HIGHAM, Stability of methods for matrix inversion, IMA J. Numer. Anal., 12 (1992), pp. 1-19. (Also LAPACK Working Note #27).

63

R. FALGOUT, A. SKJELLUM, S. SMITH, AND C. STILL, The Multicomputer Toolbox Approach to Concurrent BLAS and LACS, in Proceedings of the Scalable High Performance Computing Conference SHPCC-92, IEEE Computer Society Press, 1992.

64

M. P. I. FORUM, MPI: A message passing interface standard, International Journal of Supercomputer Applications and High Performance Computing, 8 (1994), pp. 3-4. Special issue on MPI. Also available electronically, the URL is ftp://www.netlib.org/mpi/mpi-report.ps .

65

G. FOX, M. JOHNSON, G. LYZENGA, S. OTTO, J. SALMON, AND D. WALKER, Solving Problems on Concurrent Processors, Volume 1, Prentice-Hall, Englewood Cliffs, NJ, 1988.

66

G. FOX, R. WILLIAMS, AND P. MESSINA, Parallel Computing Works!, Morgan Kaufmann Publishers, Inc., San Francisco, CA, 1994.

67

T. L. FREEMAN AND C. PHILLIPS, Parallel Numerical Algorithms, Prentice-Hall, Hemel Hempstead, Hertfordshire, UK, 1992.

68

A. GEIST, A. BEGUELIN, J. DONGARRA, W. JIANG, R. MANCHEK, AND V. SUNDERAM, PVM: Parallel Virtual Machine. A Users' Guide and Tutorial for Networked Parallel Computing, MIT Press, Cambridge, MA, 1994.

69

G. GEIST AND C. ROMINE, LU factorization algorithms on distributed memory multiprocessor architectures, SIAM J. Sci. Stat. Comput., 9 (1988), pp. 639-649.

70

G. GOLUB AND C. VAN LOAN, Matrix Computations, Johns-Hopkins, Baltimore, second ed., 1989.

71

G. GOLUB AND C. F. VAN LOAN, Matrix Computations, Johns Hopkins University Press, Baltimore, MD, third ed., 1996.

72

W. W. HAGER, Condition estimators, SIAM J. Sci. Stat. Comput., 5 (1984), pp. 311-316.

73

S. HAMMARLING, The numerical solution of the general Gauss-Markov linear model, in Mathematics in Signal Processing, T. S. et al.. Durani, ed., Clarendon Press, Oxford, UK, 1986.

74

R. HANSON, F. KROGH, AND C. LAWSON, A proposal for standard linear algebra subprograms, ACM SIGNUM Newsl., 8 (1973).

75

P. HATCHER AND M. QUINN, Data-Parallel Programming On MIMD Computers, The MIT Press, Cambridge, Massachusetts, 1991.

76

B. HENDRICKSON AND D. WOMBLE, The torus-wrap mapping for dense matrix calculations on massively parallel computers, SIAM J. Sci. Stat. Comput., 15 (1994), pp. 1201-1226.

77

G. HENRY, Improving Data Re-Use in Eigenvalue-Related Computations, PhD thesis, Cornell University, Ithaca, NY, January 1994.

78

G. HENRY AND R. VAN DE GEIJN, Parallelizing the QR algorithm for the unsymmetric algebraic eigenvalue problem: Myths and reality, SIAM J. Sci. Comput., 17 (1996), pp. 870-883. (Also LAPACK Working Note 79).

79

G. HENRY, D. WATKINS, AND J. DONGARRA, A parallel implementation of the nonsymmetric QR algorithm for distributed memory architectures, Computer Science Dept. Technical Report CS-97-352, University of Tennessee, Knoxville, TN, March 1997. (Also LAPACK Working Note # 121).

80

N. J. HIGHAM, A survey of condition number estimation for triangular matrices, SIAM Review, 29 (1987), pp. 575-596.

81

height 2pt depth -1.6pt width 23pt, FORTRAN codes for estimating the one-norm of a real or complex matrix, with applications to condition estimation, ACM Trans. Math. Softw., 14 (1988), pp. 381-396.

82

height 2pt depth -1.6pt width 23pt, Experience with a matrix norm estimator, SIAM J. Sci. Stat. Comput., 11 (1990), pp. 804-809.

83

height 2pt depth -1.6pt width 23pt, Perturbation theory and backward error for AX-XB=C, BIT, 33 (1993), pp. 124-136.

84

height 2pt depth -1.6pt width 23pt, Accuracy and Stability of Numerical Algorithms, Society for Industrial and Applied Mathematics, Philadelphia, PA, 1996.

85

S. HUSS-LEDERMAN, E. JACOBSON, A. TSAO, AND G. ZHANG, Matrix Multiplication on the Intel Touchstone DELTA, Concurrency: Practice and Experience, 6 (1994), pp. 571-594.

86

S. HUSS-LEDERMAN, A. TSAO, AND G. ZHANG, A parallel implementation of the invariant subspace decomposition algorithm for dense symmetric matrices, in Proceedings of the Sixth SIAM Conference on Parallel Processing for Scientific Computing, SIAM, 1993, pp. 367-374.

87

K. HWANG, Advanced Computer Architecture: Parallelism, Scalability, Programmability, McGraw-Hill, 1993.

88

IBM CORPORATION, IBM RS6000, 1996. (URL = http://www.rs6000.ibm.com/).

89

INTEL CORPORATION, Intel Supercomputer Technical Publications Home Page, 1995. (URL = http://www.ssd.intel.com/pubs.html).

90

B. KåGSTRfOM, P. LING, AND C. V. LOAN, GEMM-based level 3 BLAS: High-performance model implementations and performance evaluation benchmark, Tech. Rep. UMINF 95-18, Department of Computing Science, Umeå University, 1995. Submitted to ACM Trans. Math. Softw.

91

C. KOEBEL, D. LOVEMAN, R. SCHREIBER, G. STEELE, AND M. ZOSEL, The High Performance Fortran Handbook, MIT Press, Cambridge, Massachusetts, 1994.

92

V. KUMAR, A. GRAMA, A. GUPTA, AND G. KARYPIS, Introduction to Parallel Computing - Design and Analysis of Algorithms, The Benjamin/Cummings Publishing Company, Inc., Redwood City, CA, 1994.

93

C. L. LAWSON, R. J. HANSON, D. KINCAID, AND F. T. KROGH, Basic linear algebra subprograms for Fortran usage, ACM Trans. Math. Soft., 5 (1979), pp. 308-323.

94

R. LEHOUCQ, The computation of elementary unitary matrices, Computer Science Dept. Technical Report CS-94-233, University of Tennessee, Knoxville, TN, 1994. (Also LAPACK Working Note 72).

95

T. LEWIS AND H. EL-REWINI, Introduction to Parallel Computing, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1992.

96

X. LI, Sparse Gaussian Elimination on High Performance Computers, PhD thesis, Computer Science Division, Department of Electrical Engineering and Computer Science, University of California, Berkeley, CA, September 1996.

97

W. LICHTENSTEIN AND S. L. JOHNSSON, Block-cyclic dense linear algebra, SIAM J. Sci. Stat. Comput., 14 (1993), pp. 1259-1288.

98

A. MAINWARING AND D. E. CULLER, Active message applications programming interface and communication subsystem organization, Tech. Rep. UCB CSD-96-918, University of California at Berkeley, Berkeley, CA, October 1996.

99

P. PACHECO, Parallel Programming with MPI, Morgan Kaufmann Publishers, Inc., San Francisco, CA, 1997.

100

C. PAIGE, Some aspects of generalized QR factorization, in Reliable Numerical Computations, M. Cox and S. Hammarling, eds., Clarendon Press, 1990.

101

B. PARLETT, The Symmetric Eigenvalue Problem, Prentice-Hall, Englewood Cliffs, NJ, 1980.

102

height 2pt depth -1.6pt width 23pt, The construction of orthogonal eigenvectors for tight clusters by use of submatrices, Center for Pure and Applied Mathematics PAM-664, University of California, Berkeley, CA, January 1996. submitted to SIMAX.

103

B. PARLETT AND I. DHILLON, On Fernando's method to find the most redundant equation in a tridiagonal system, Linear Algebra and Its Applications, (1996). to appear.

104

A. PETITET, Algorithmic Redistribution Methods for Block Cyclic Decompositions, PhD thesis, University of Tennessee, Knoxville, TN, 1996.

105

E. POLLICINI, A. A., Using Toolpack Software Tools, 1989.

106

L. PRYLLI AND B. TOURANCHEAU, Efficient block cyclic data redistribution, in EUROPAR'96, vol. 1 of Lecture Notes in Computer Science, Springer-Verlag, 1996, pp. 155-165.

107

height 2pt depth -1.6pt width 23pt, Efficient block cyclic array redistribution, Journal of Parallel and Distributed Computing, (1997). To appear.

108

R. SCHREIBER AND C. F. VAN LOAN, A storage efficient WY representation for products of Householder transformations, SIAM J. Sci. Stat. Comput., 10 (1989), pp. 53-57.

109

B. SMITH, W. GROPP, AND L. CURFMAN MCINNES, PETSc 2.0 users manual, Technical Report ANL-95/11, Argonne National Laboratory, Argonne, IL, 1995. (Available by anonymous ftp from ftp.mcs.anl.gov).

110

M. SNIR, S. W. OTTO, S. HUSS-LEDERMAN, D. W. WALKER, AND J. J. DONGARRA, MPI: The Complete Reference, MIT Press, Cambridge, MA, 1996.

111

SUNSOFT, The XDR Protocol Specification. Appendix A of ``Network Interfaces Programmer's Guide'', SunSoft, 1993.

112

E. VAN DE VELDE, Concurrent Scientific Computing, no. 16 in Texts in Applied Mathematics, Springer-Verlag, 1994.

113

R. C. WHALEY, Basic linear algebra communication subprograms: Analysis and implementation across multiple parallel architectures, Computer Science Dept. Technical Report CS-94-234, University of Tennessee, Knoxville, TN, May 1994. (Also LAPACK Working Note 73).

114

J. H. WILKINSON, The Algebraic Eigenvalue Problem, Oxford University Press, Oxford, UK, 1965.