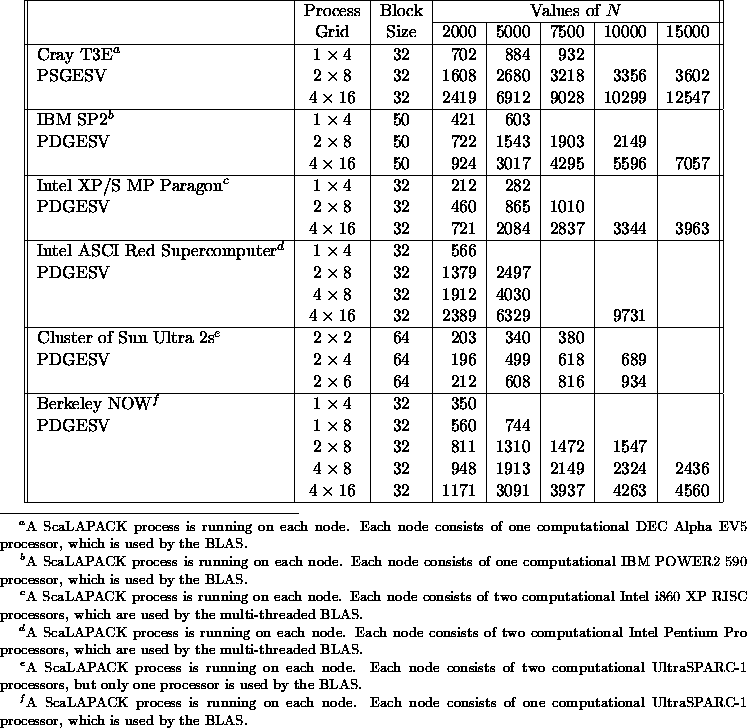
Table 5.9: Speed in Mflop/s of PSGESV/PDGESV for square matrices of order N
Table 5.9 illustrates the speed of the ScaLAPACK driver routine PSGESV /PDGESV for solving a square linear system of order N by LU factorization with partial row pivoting of a real matrix. For all timings, 64-bit floating-point arithmetic was used. Thus, single-precision timings are reported for the Cray T3E, and double precision timings are reported on all other computers. The distribution block size is also used as the partitioning unit for the computation and communication phases.
Table 5.10 illustrates the speed of the ScaLAPACK routine PSPOSV /PDPOSV for solving a symmetric positive definite linear system of order N via the Cholesky factorization.
Right-looking variants of the LU and Cholesky factorizations were chosen for ScaLAPACK because they minimize total communication volume, that is, the aggregated

Table 5.9: Speed in Mflop/s of PSGESV/PDGESV for square
matrices of order N
amount of data transferred between processes during the operation.
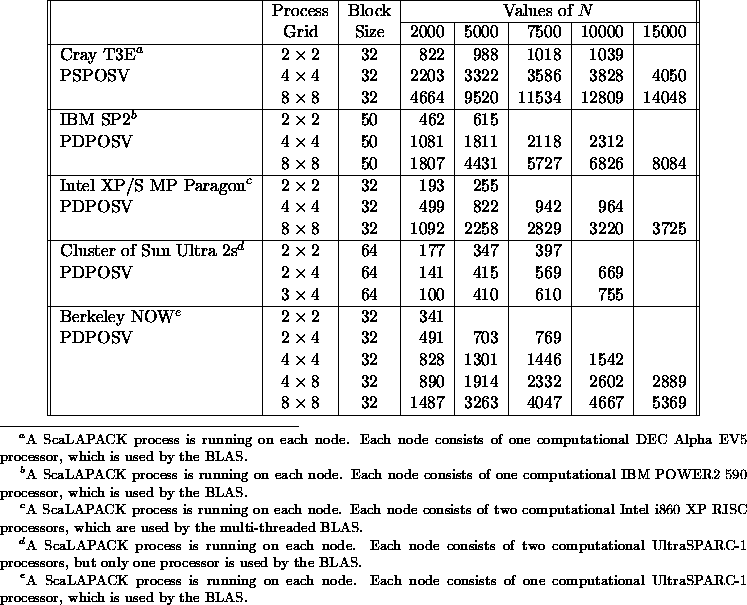
Table 5.10: Speed in Mflop/s of PSPOSV/PDPOSV for matrices of
order N with UPLO=`U'