




Next: Solving Linear Systems of
Up: Performance of Selected BLACS
Previous: Performance of Selected PBLAS
This section contains performance numbers for selected driver
routines. These routines provide complete solutions for common
linear algebra problems.
- Solve a general N-by-N system of linear equations
with one right-hand side using the routine PSGESV/PDGESV.
- Solve a symmetric positive definite N-by-N system of
linear equations with one right-hand side, using PSPOSV/PDPOSV.
- Solve an N-by-N linear least squares problem
with one right-hand side using the routine PSGELS/PDGELS.
- Find the eigenvalues and optionally the corresponding
eigenvectors of an N-by-N symmetric matrix, using the
routine PSSYEVX/PDSYEVX.
- Find the eigenvalues and optionally the corresponding
eigenvectors of an N-by-N symmetric matrix, using the
routine PSSYEV/PDSYEV.
- Find the singular values and optionally the corresponding
right and left singular vectors of an N-by-N matrix,
using PSGESVD/PDGESVD.
- Find the eigenvalues and optionally the
corresponding right eigenvectors of an N-by-N
Hessenberg matrix, using the routine PSLAHQR/PDLAHQR.

Table 5.8
presents ``standard'' floating-point
operation costs
(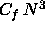 ) for selected ScaLAPACK drivers for matrices
of order N. Approximate values of the constants
) for selected ScaLAPACK drivers for matrices
of order N. Approximate values of the constants
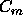 and
and 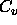 defined in section 5.2.3
are also provided.
defined in section 5.2.3
are also provided.
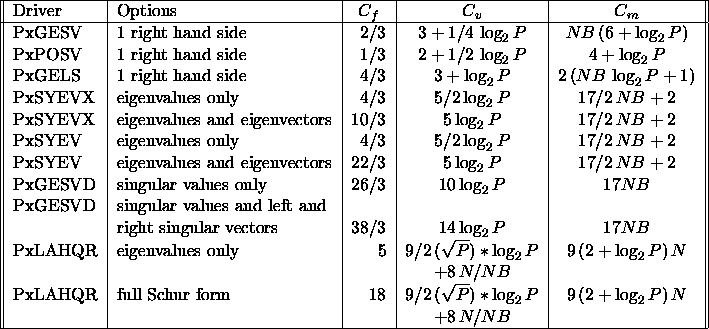
Table 5.8: ``Standard'' floating-point operation (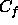 ) and communication
costs (
) and communication
costs (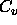 ,
, 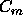 ) for selected ScaLAPACK drivers
) for selected ScaLAPACK drivers
The operation counts given for the eigenvalue and SVD drivers
are incomplete. They do not include any of the 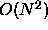 computation
costs (i.e., the entire tridiagonal eigendecomposition is ignored in
PxxxEVX). Furthermore, the reductions involved require matrix-vector
multiplies, which are less efficient than the matrix-matrix multiplies
required by the other drivers listed here.
Hence this table greatly underestimates the execution time
of the eigenvalue and SVD drivers, especially the expert symmetric eigensolver drivers.
For PxLAHQR, when only eigenvalues are computed,
computation
costs (i.e., the entire tridiagonal eigendecomposition is ignored in
PxxxEVX). Furthermore, the reductions involved require matrix-vector
multiplies, which are less efficient than the matrix-matrix multiplies
required by the other drivers listed here.
Hence this table greatly underestimates the execution time
of the eigenvalue and SVD drivers, especially the expert symmetric eigensolver drivers.
For PxLAHQR, when only eigenvalues are computed, 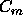 and
and 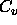 look the same as the full Schur form case, in terms of ``order of
magnitude''. There is actually
look the same as the full Schur form case, in terms of ``order of
magnitude''. There is actually 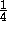 to
to 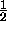 the
number of messages/volume depending on the circumstances.
the
number of messages/volume depending on the circumstances.





Next: Solving Linear Systems of
Up: Performance of Selected BLACS
Previous: Performance of Selected PBLAS
Susan Blackford
Tue May 13 09:21:01 EDT 1997

![]() ) and communication
costs (
) and communication
costs (![]() ,
, ![]() ) for selected ScaLAPACK drivers
) for selected ScaLAPACK drivers![]() computation
costs (i.e., the entire tridiagonal eigendecomposition is ignored in
PxxxEVX). Furthermore, the reductions involved require matrix-vector
multiplies, which are less efficient than the matrix-matrix multiplies
required by the other drivers listed here.
Hence this table greatly underestimates the execution time
of the eigenvalue and SVD drivers, especially the expert symmetric eigensolver drivers.
For PxLAHQR, when only eigenvalues are computed,
computation
costs (i.e., the entire tridiagonal eigendecomposition is ignored in
PxxxEVX). Furthermore, the reductions involved require matrix-vector
multiplies, which are less efficient than the matrix-matrix multiplies
required by the other drivers listed here.
Hence this table greatly underestimates the execution time
of the eigenvalue and SVD drivers, especially the expert symmetric eigensolver drivers.
For PxLAHQR, when only eigenvalues are computed, ![]() and
and ![]() look the same as the full Schur form case, in terms of ``order of
magnitude''. There is actually
look the same as the full Schur form case, in terms of ``order of
magnitude''. There is actually ![]() to
to ![]() the
number of messages/volume depending on the circumstances.
the
number of messages/volume depending on the circumstances.