The efficiency of the ScaLAPACK software depends
on efficient implementations of the BLAS and the BLACS being
provided by computer vendors (or others) for their computers.
The BLAS and the BLACS form a low-level interface between
ScaLAPACK software and different computer architectures.
Table 5.5 presents performance numbers indicating
how well the BLACS and Level 3 BLAS perform on different
distributed-memory computers. For each computer this table shows the
flop rate achieved by the matrix-matrix multiply Level 3 BLAS
routine SGEMM/DGEMM (
) on a node versus the theoretical
peak performance of that node,
the underlying message-passing library
called by the BLACS,
and the approximated values of the latency (
) and the
bandwidth (
) achieved by the BLACS versus the
underlying message-passing software for the machine.
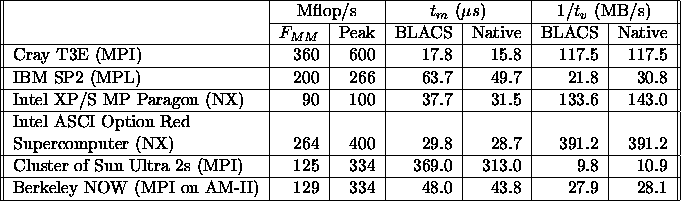
Table 5.5: BLACS and Level 3 BLAS performance indicators
The values for latency in table 5.5 were obtained by timing the cost of a 0-byte message. The bandwidth numbers table 5.5 were obtained by increasing message length until message bandwidth was saturated. We used the same timing mechanism for both the BLACS and the underlying message-passing library.
These numbers are actual timing numbers, not values based on hardware peaks, for instance. Therefore, they should be considered as approximate values or indicators of the observed performance between two nodes, as opposed to precise evaluations of the interconnection network capabilities. On the CRAY, the numbers reported are for MPI and the MPIBLACS, instead of the more optimal shmem library with CRAY's native BLACS.
For all four computers, a machine-specific optimized BLAS
implementation was used for all the performance numbers reported
in this chapter. For the IBM Scalable POWERparallel 2 (SP2)
computer, the IBM Engineering and Scientific Subroutine Library (ESSL)
was used [88]. On the Intel XP/S MP Paragon computer, the Intel
Basic Math Library Software (Release 5.0) [89] was used.
On the Sun Ultra Enterprise 2
workstation, the Dakota Scientific Software Library (DSSL)
was used. The DSSL BLAS implementation used only one processor
per node. The speed of the BLAS matrix-matrix multiply routine shown
in Table 5.5 has been obtained for the following
operation 
,
where A, B, and C are square matrices of order 500.