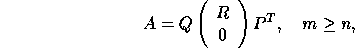
To solve a linear least squares problem (2.1) when A is not of full rank, or the rank of A is in doubt, we can perform either a QR factorization with column pivoting or a singular value decomposition (see subsection 2.3.6).
The QR factorization with column pivoting is given by
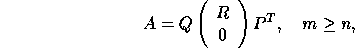
where Q and R are as before and P is a permutation matrix, chosen (in general) so that
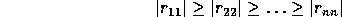
and moreover, for each k,
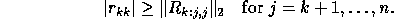
In exact arithmetic, if rank(A) = k, then the whole of the submatrix
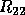in rows and columns k + 1 to n
would be zero. In numerical computation, the aim must be to
determine an index k, such that the leading submatrix 
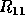in the first
k rows and columns is well-conditioned, and 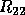is negligible:
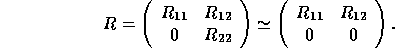
Then k is the effective rank of A. See Golub and Van Loan [45] for a further discussion of numerical rank determination.
The so-called basic solution to the linear least squares problem (2.1) can be obtained from this factorization as
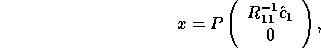
where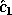 
consists of just the first k elements of 
.
The routine xGEQPF computes the QR factorization with column pivoting, but does not attempt to determine the rank of A. The matrix Q is represented in exactly the same way as after a call of xGEQRF , and so the routines xORGQR and xORMQR can be used to work with Q (xUNGQR and xUNMQR if Q is complex).