References





Next: Index
Up: LAPACK Users' Guide Release
Previous: Notes
References
- 1
-
E. ANDERSON, Z. BAI, C. BISCHOF, J. W. DEMMEL, J. J. DONGARRA, J. DU CROZ,
A. GREENBAUM, S. HAMMARLING, A. MCKENNEY, AND D. SORENSEN, LAPACK: A
portable linear algebra library for high-performance computers, Computer
Science Dept. Technical Report CS-90-105, University of Tennessee,
Knoxville, 1990.
(LAPACK Working Note 20).
- 2
-
E. ANDERSON, Z. BAI, AND J. J. DONGARRA,
Generalized QR Factorization and its Applications,
Computer Science Dept. Technical Report CS-91-131,
University of Tennessee, Knoxville, 1991.
(LAPACK Working Note 31).
- 3
-
E. ANDERSON, J. J. DONGARRA, AND S. OSTROUCHOV, Installation guide
for LAPACK, Computer Science Dept. Technical Report CS-92-151,
University of Tennessee, Knoxville, 1992.
(LAPACK Working Note 41).
- 4
-
ANSI/IEEE, IEEE Standard for Binary Floating-Point Arithmetic, New York, Std
754-1985 ed., 1985.
- 5
-
ANSI/IEEE, IEEE Standard for Radix Independent Floating Point Arithmetic,
New York, Std 854-1987 ed., 1987.
- 6
-
M. ARIOLI, J. W. DEMMEL, AND I. S. DUFF, Solving sparse linear
systems with sparse backward error, SIAM J. Matrix Anal. Appl., 10 (1989),
pp. 165-190.
- 7
-
M. ARIOLI, I. S. DUFF, AND P. P. M. DE RIJK, On the augmented system
approach to sparse least squares problems, Num. Math., 55 (1989),
pp. 667-684.
- 8
-
Z. BAI AND J. W. DEMMEL, On a block implementation of Hessenberg
multishift QR iteration, Int. J. of High Speed Comput., 1
(1989), pp. 97-112.
(LAPACK Working Note 8).
- 9
-
Z. BAI AND J. W. DEMMEL,
Design of a parallel nonsymmetric eigenroutine toolbox, Part I,
Proceedings of the Sixth SIAM Conference on Parallel Proceesing for Scientific
Computing, SIAM (1993), pp. 391-398.
- 10
-
Z. BAI AND J. W. DEMMEL,
Computing the generalized singular value decomposition,
SIAM J. Sci. Comp., 14 (1993), pp. 1464-1486.
(LAPACK Working Note 46).
- 11
-
Z. BAI, J. W. DEMMEL, AND A. MCKENNEY, On computing condition
numbers for the nonsymmetric eigenproblem, ACM Trans. Math. Soft. 19
(1993), pp. 202-223.
(LAPACK Working Note 13).
- 12
-
Z. BAI AND H. ZHA,
A new preprocessing algorithm for the computation of the
generalized singular value decomposition,
SIAM J. Sci. Comp., 14 (1993), pp. 1007-1012.
- 13
-
J. BARLOW AND J. DEMMEL, Computing accurate eigensystems of scaled
diagonally dominant matrices, SIAM J. Num. Anal., 27 (1990), pp. 762-791.
(LAPACK Working Note 7).
- 14
-
C. R. CRAWFORD,
Reduction of a band-symmetric generalized eigenvalue problem,
Comm. ACM, 16 (1973), pp. 41-44.
- 15
-
J. J. M. CUPPEN,
A divide and conquer method for the symmetric tridiagonal eigenproblem,
Numerische Math., 36 (1981), pp. 177-195.
- 16
-
P. DEIFT, J. W. DEMMEL, L.-C. LI, AND C. TOMEI, The bidiagonal
singular value decomposition and Hamiltonian mechanics, SIAM J. Num.
Anal., 28 (1991), pp. 1463-1516.
(LAPACK Working Note 11).
- 17
-
J. W. DEMMEL, The Condition Number of Equivalence Transformations
that Block Diagonalize Matrix Pencils,
SIAM J. Num. Anal., 20 (1983), pp. 599-610.
- 18
-
J. W. DEMMEL, Underflow and the
Reliability of Numerical Software, SIAM J. Sci. Stat. Comput., 5 (1984),
pp. 887-919.
- 19
-
J. W. DEMMEL AND N. J. HIGHAM, Improved error bounds for
underdetermined systems solvers, SIAM J. Matrix Anal. Appl., 14 (1993),
pp. 1-14.
- 20
-
J. W. DEMMEL AND N. J. HIGHAM, Stability of block
algorithms with fast level 3 BLAS, ACM Trans. Math. Soft., 18 (1992),
pp. 274-291.
(LAPACK Working Note 22).
- 21
-
J. W. DEMMEL AND B. KåGSTRÖM, Computing Stable
Eigendecompositions of Matrix Pencils, Lin. Alg. Appl., 88/89 (1987),
pp. 139-186.
- 22
-
J. W. DEMMEL AND W. KAHAN, Accurate singular values of bidiagonal
matrices, SIAM J. Sci. Stat. Comput., 11 (1990), pp. 873-912.
(LAPACK Working Note 3).
- 23
-
J. W. DEMMEL AND X. LI,
Faster Numerical Algorithms via Exception Handling,
IEEE Trans. Comp., 43 (1994), pp. 983-992.
(LAPACK Working Note 59).
- 24
-
J. W. DEMMEL AND K. VESELIC, Jacobi's method is more accurate
than QR, SIAM J. Matrix Anal. Appl. 13 (1992), pp. 1204-1246.
(LAPACK Working Note 15).
- 25
-
B. DE MOOR AND P. VAN DOOREN,
Generalization of the singular value and QR decompositions,
SIAM J. Matrix Anal. Appl., 13 (1992), pp. 993-1014.
- 26
-
J. J. DONGARRA, J. R. BUNCH, C. B. MOLER, AND G. W. STEWART, LINPACK
Users' Guide, SIAM, Philadelphia, PA, 1979.
- 27
-
J. J. DONGARRA, J. DU CROZ, I. S. DUFF, AND S. HAMMARLING, Algorithm
679: A set of Level 3 Basic Linear Algebra Subprograms, ACM
Trans. Math. Soft., 16 (1990), pp. 18-28.
- 28
-
J. J. DONGARRA, J. DU CROZ, I. S. DUFF, AND S. HAMMARLING, A set of Level 3
Basic Linear Algebra Subprograms, ACM Trans. Math. Soft., 16
(1990), pp. 1-17.
- 29
-
J. J. DONGARRA, J. DU CROZ, S. HAMMARLING, AND R. J. HANSON, Algorithm 656: An extended set of FORTRAN Basic Linear Algebra
Subprograms, ACM Trans. Math. Soft., 14 (1988), pp. 18-32.
- 30
-
J. J. DONGARRA, J. DU CROZ, S. HAMMARLING, AND R. J. HANSON, An extended set of
FORTRAN Basic Linear Algebra Subprograms, ACM Trans. Math. Soft., 14
(1988), pp. 1-17.
- 31
-
J. J. DONGARRA, I. S. DUFF, D. C. SORENSEN, AND H. A. VAN DER VORST, Solving Linear Systems on Vector and Shared Memory Computers, SIAM
Publications, 1991.
- 32
-
J. J. DONGARRA AND E. GROSSE, Distribution of mathematical software
via electronic mail, Communications of the ACM, 30 (1987), pp. 403-407.
- 33
-
J. J. DONGARRA, F. G. GUSTAFSON, AND A. KARP, Implementing linear
algebra algorithms for dense matrices on a vector pipeline machine, SIAM
Review, 26 (1984), pp. 91-112.
- 34
-
J. J. DONGARRA, S. HAMMARLING, AND D. C. SORENSEN, Block reduction
of matrices to condensed forms for eigenvalue computations, JCAM, 27
(1989), pp. 215-227.
(LAPACK Working Note 2).
- 35
-
J. J. DONGARRA AND S. OSTROUCHOV, Quick installation guide
for LAPACK on unix systems, Computer Science Dept. Technical
Report CS-94-249, University of Tennessee, Knoxville, 1994.
(LAPACK Working Note 81).
- 36
-
J. J. DONGARRA, R. POZO, AND D. WALKER,
An object oriented design for high performance linear algebra on
distributed memory architectures, Computer Science Dept. Technical
Report CS-93-200, University of Tennessee, Knoxville, 1993.
(LAPACK Working Note 61).
- 37
-
A. DUBRULLE, The multishift QR algorithm: is it worth the
trouble?, Palo Alto Scientific Center Report G320-3558x, IBM Corp.,
Palo Alto, 1991.
- 38
-
J. DU CROZ AND N. J. HIGHAM, Stability of methods for matrix
inversion, IMA J. Num. Anal., 12 (1992), pp. 1-19.
(LAPACK Working Note 27).
- 39
-
J. DU CROZ, P. J. D. MAYES, AND G. RADICATI DI BROZOLO, Factorizations of band matrices using Level 3 BLAS, Computer Science
Dept. Technical Report CS-90-109, University of Tennessee, Knoxville,
1990.
(LAPACK Working Note 21).
- 40
-
S. I. FELDMAN, D. M. GAY, M. W. MAIMONE, AND N. L. SCHRYER,
A Fortran-to-C Converter, Computing Science Technical
Report No. 149, AT & T Bell Laboratories, Murray Hill, NJ, 1990.
- 41
-
V. FERNANDO AND B. PARLETT,
Accurate singular values and differential qd algorithms,
Numerisch Math. 67 (1994), pp. 191-229.
- 42
-
K. A. GALLIVAN, R. J. PLEMMONS, AND A. H. SAMEH, Parallel algorithms
for dense linear algebra computations, SIAM Review, 32 (1990),
pp. 54-135.
- 43
-
F. GANTMACHER,
The Theory of Matrices, vol. II (transl.),
Chelsea Publishers, New York, 1959.
- 44
-
B. S. GARBOW, J. M. BOYLE, J. J. DONGARRA, AND C. B. MOLER, Matrix
Eigensystem Routines - EISPACK Guide Extension, vol. 51 of Lecture Notes
in Computer Science, Springer-Verlag, Berlin, 1977.
- 45
-
G. GOLUB AND C. F. VAN LOAN, Matrix Computations, Johns Hopkins
University Press, Baltimore, MD, 2nd ed., 1989.
- 46
-
A. GREENBAUM AND J. J. DONGARRA, Experiments with QL/QR methods
for the symmetric tridiagonal eigenproblem, Computer Science Dept.
Technical Report CS-89-92, University of Tennessee, Knoxville, 1989.
(LAPACK Working Note 17).
- 47
-
M. GU AND S. EISENSTAT,
A stable algorithm for the rank-1 modification of the symmetric
eigenproblem, Yale University, Computer Science Department Report
YALEU/DCS/RR-916, New Haven, CT (1992).
- 48
-
W. W. HAGER, Condition estimators, SIAM J. Sci. Stat. Comput., 5
(1984), pp. 311-316.
- 49
-
S. HAMMARLING,
The numerical solution of the general Gauss-Markov
linear model, in Mathematics in Signal Processing,
eds. T. S. Durrani et al., Clarendon Press, Oxford
(1986).
- 50
-
N. J. HIGHAM, Efficient algorithms for computing the condition
number of a tridiagonal matrix, SIAM J. Sci. Stat. Comput., 7 (1986),
pp. 150-165.
- 51
-
N. J. HIGHAM, A survey of
condition number estimation for triangular matrices, SIAM Review, 29
(1987), pp. 575-596.
- 52
-
N. J. HIGHAM, FORTRAN codes for
estimating the one-norm of a real or complex matrix, with applications to
condition estimation, ACM Trans. Math. Soft., 14 (1988), pp. 381-396.
- 53
-
N. J. HIGHAM, Experience with a
matrix norm estimator, SIAM J. Sci. Stat. Comput., 11 (1990),
pp. 804-809.
- 54
-
N. J. HIGHAM, Perturbation Theory
and Backward Error for AX-XB=C., BIT, 33 (1993), pp. 124-136.
- 55
-
S. HUSS-LEDERMAN, A. TSAO AND G. ZHANG,
A parallel implementation of the invariant subspace
decomposition algorithm for dense symmetric matrices,
in Proceedings of the Sixth SIAM Conference on Parallel Processing for
Scientific Computing, SIAM (1993), pp. 367-374.
- 56
-
T. KATO, Perturbation Theory for Linear Operators, Springer Verlag,
Berlin, 2 ed., 1980.
- 57
-
L. KAUFMAN,
Banded eigenvalue solvers on vector machines,
ACM Trans. Math. Soft., 10 (1984), pp. 73-86.
- 58
-
C. L. LAWSON, R. J. HANSON, D. KINCAID, AND F. T. KROGH, Basic
Linear Algebra Subprograms for FORTRAN usage, ACM Trans. Math. Soft., 5
(1979), pp. 308-323.
- 59
-
R. LEHOUCQ, The computation of elementary unitary matrices,
Computer Science Dept. Technical Report CS-94-233, University
of Tennessee, Knoxville, 1994.
(LAPACK Working Note 72).
- 60
-
C. PAIGE,
Fast numerically stable computations for generalized linear least
squares problems,
SIAM J. Num. Anal., 16 (1979), pp. 165-179.
- 61
-
C. PAIGE,
A note on a result of Sun Ji-guang: sensitivity of the
CS and GSV decomposition,
SIAM J. Num. Anal., 21 (1984), pp. 186-191.
- 62
-
C. PAIGE,
Computing the generalized singular value decomposition,
SIAM J. Sci. Stat. Comput., 7 (1986), pp. 1126-1146.
- 63
-
C. PAIGE,
Some aspects of generalized QR factorization,
in Reliable Numerical Computations, eds. M. Cox and S. Hammarling,
Clarendon Press, Oxford (1990).
- 64
-
B. PARLETT, The Symmetric Eigenvalue Problem, Prentice Hall,
Englewood Cliffs, NJ, 1980.
- 65
-
M. PAYNE AND B. WICHMANN,
Language Independent Arithmetic (LIA) - Part 1:
Integer and floating point arithmetic,
International Standards Organization, ISO/IEC 10967-1:1994, 1994.
- 66
-
A. A. POLLICINI, ed., Using Toolpack Software Tools, Kluwer
Academic, 1989.
- 67
-
J. RUTTER,
A serial implementation of Cuppen's Divide and Conquer Algorithm for
the Symmetric Tridiagonal Eigenproblem,
University of California, Computer Science Division Report
UCB/CSD 94/799, Berkeley CA (1994).
(LAPACK Working Note 69).
- 68
-
R. SCHREIBER AND C. F. VAN LOAN, A storage efficient WY
representation for products of Householder transformations, SIAM J. Sci.
Stat. Comput., 10 (1989), pp. 53-57.
- 69
-
I. SLAPNICAR, Accurate symmetric eigenreduction by a
Jacobi method, PhD dissertation, Fernuniversität - Hagen,
Hagen, Germany, 1992.
- 70
-
B. T. SMITH, J. M. BOYLE, J. J. DONGARRA, B. S. GARBOW, Y. IKEBE, V. C.
KLEMA, AND C. B. MOLER, Matrix Eigensystem Routines - EISPACK
Guide, vol. 6 of Lecture Notes in Computer Science, Springer-Verlag, Berlin,
2 ed., 1976.
- 71
-
G. W. STEWART, On the sensitivity of the eigenvalue problem
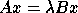 , SIAM J. Num. Anal., 9 (1972), pp. 669-686.
, SIAM J. Num. Anal., 9 (1972), pp. 669-686.
- 72
-
G. W. STEWART, Error and perturbation bounds for subspaces
associated with certain eigenvalue problems, SIAM Review, 15 (1973),
pp. 727-764.
- 73
-
G. W. STEWART AND J.-G. SUN, Matrix Perturbation Theory, Academic
Press, New York, 1990.
- 74
-
J.-G. SUN,
Perturbation analysis for the generalized singular value problem,
SIAM J. Num. Anal., 20 (1983), pp. 611-625.
- 75
-
J. VARAH, On the separation of two matrices, SIAM J. Num. Anal.,
16 (1979), pp. 216-222.
- 76
-
K. VESELIC AND I. SLAPNICAR,
Floating point perturbations of Hermitian matrices,
Linear Algebra Appl., to appear.
- 77
-
D. S. WATKINS AND L. ELSNER, Convergence of algorithms of
decomposition type for the eigenvalue problem, Linear Algebra Appl. 143 (1991),
pp. 19-47.
- 78
-
J. H. WILKINSON, The Algebraic Eigenvalue Problem, Oxford
University Press, Oxford, 1965.
- 79
-
J. H. WILKINSON,
Some recent advances in numerical linear algebra,
in: D. A. H. JACOBS, ed., The State of the Art in Numerical
Analysis, Academic Press, New York, 1977.
- 80
-
J. H. WILKINSON, Kronecker's canonical form and the QZ
algorithm, Lin. Alg. Appl., 28 (1979), pp. 285-303.
- 81
-
J. H. WILKINSON AND C. REINSCH, eds., Handbook for Automatic
Computation, vol 2.: Linear Algebra, Springer-Verlag, Heidelberg,
1971.
Tue Nov 29 14:03:33 EST 1994
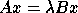 , SIAM J. Num. Anal., 9 (1972), pp. 669-686.
, SIAM J. Num. Anal., 9 (1972), pp. 669-686.
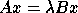 , SIAM J. Num. Anal., 9 (1972), pp. 669-686.
, SIAM J. Num. Anal., 9 (1972), pp. 669-686.