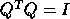LAPACK provides a number of routines for factorizing a general rectangular m-by-n matrix A, as the product of an orthogonal matrix (unitary if complex) and a triangular (or possibly trapezoidal) matrix.
A real matrix Q is orthogonal if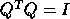 
;
a complex matrix Q is unitary if 
.
Orthogonal or unitary matrices have the important property that they leave the
two-norm of a vector invariant:
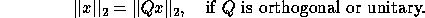
As a result, they help to maintain numerical stability because they do not amplify rounding errors.
Orthogonal factorizations are used in the solution of linear least squares problems . They may also be used to perform preliminary steps in the solution of eigenvalue or singular value problems.